Вы когда-нибудь задумывались о том, как точно рассчитать припуск на изгиб для ваших проектов по изготовлению металлоконструкций? В этой статье блога мы исследуем увлекательный мир формул и расчетов припусков на изгиб. Как опытный инженер-механик, я расскажу вам о ключевых понятиях и дам практические советы, которые помогут вам освоить этот важнейший аспект проектирования листового металла. Приготовьтесь погрузиться в работу и раскрыть секреты создания точных и эффективных изгибов в ваших проектах!
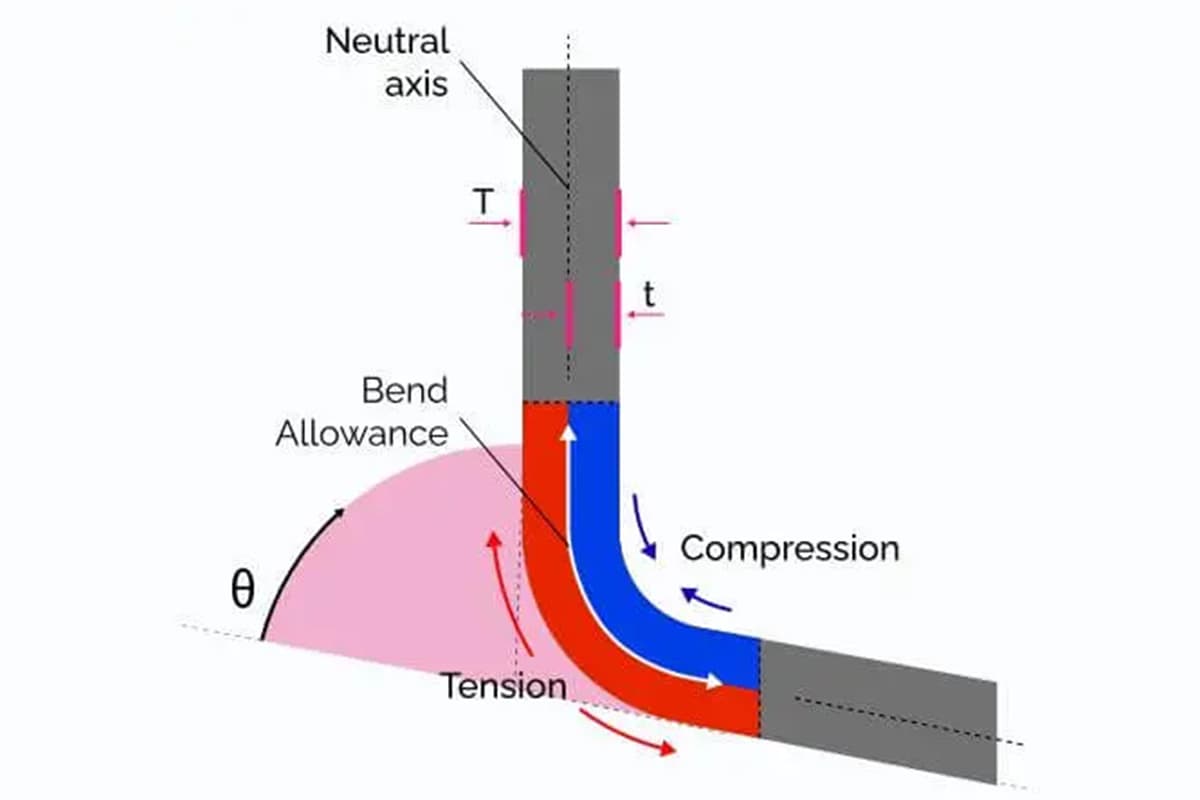
Припуск на изгиб - важнейшее понятие в области производства листового металла, особенно при работе с гибочными операциями. Он обозначает дополнительную длину материала, необходимую для размещения изгиба в металлическом листе. Понимание и точный расчет припуска на изгиб очень важны для обеспечения соответствия конечных размеров гнутой детали проектным спецификациям.
Точные расчеты припусков на изгиб крайне важны в процессе изготовления. Когда плоский металлический лист сгибается, материал на внешней стороне сгиба растягивается, а материал на внутренней стороне сжимается. Без учета этой деформации конечный продукт не будет соответствовать задуманному дизайну, что приведет к неточностям и возможным поломкам. Припуск на изгиб помогает изготовителям скорректировать размеры плоской детали, гарантируя, что согнутая деталь будет точно соответствовать требованиям.
На расчеты припусков на изгиб влияют несколько критических параметров:
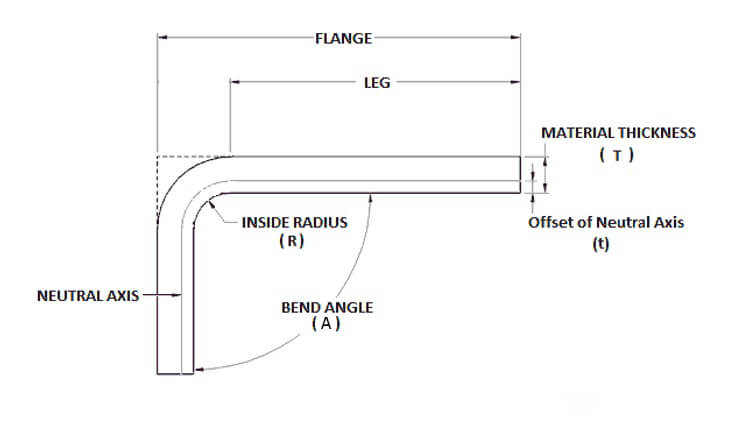
Концепция припуск на изгиб Это выглядит следующим образом: когда лист металла сгибается, он имеет три размера - два внешних (L1 и L2) и один размер толщины (T).
Важно отметить, что сумма L1 и L2 больше, чем длина в развернутом виде (L), а разница между ними называется припуском на изгиб (K).
Таким образом, длина изгиба в развернутом виде может быть рассчитана как L = L1 + L2 - K.
Похожие статьи:
Как была получена формула для припуск на изгиб создан? И как вы рассчитываете припуск на изгиб?
Припуск на изгиб зависит от внутреннего радиуса формы. Нижнее V-образное отверстие штампа определяет внутренний радиус (I.R.) формируемой детали. Внутренний радиус для низкоуглеродистой стали равен 5/32 x нижнее V отверстие штампа (W), если радиус пуансона меньше 5/32 x W.
Если I.R.< Толщина материала (t)
Если I.R.> 2 x Толщина материала (t)
Где A= (180 - угол изгиба)
Если внутренний радиус равен t или 2t, или находится между t и 2t, припуск на изгиб рассчитывается путем интерполяции значений припуска на изгиб из двух вышеупомянутых формул.
Кроме того, для расчета припуска на изгиб можно воспользоваться следующей формулой:
Эта формула учитывает различные геометрические параметры и свойства формируемых деталей.
Толщина материала (T), угол изгиба (A), внутренний радиус изгиба (R) и коэффициент K материала, который необходимо согнуть, являются наиболее важными факторами в этом расчете.
Как видно из приведенной выше формулы, расчет припуска на изгиб является простым процессом.
Вы можете определить припуск на изгиб, подставив вышеупомянутые значения в формулу.
Если угол изгиба составляет 90°, формула припуска на изгиб может быть упрощена следующим образом:
Примечание: Коэффициент K для большинства стандартных материалов и толщин обычно находится в диапазоне от 0 до 0,5.
Вы можете точно рассчитать значение коэффициента K, используя следующее Калькулятор коэффициента K:
Формула припуска на изгиб (BA) необходима для расчета длины материала, требуемой для формирования изгиба. Эта общая формула широко применима к различным материалам и методам гибки:
Где:
Коэффициент K имеет решающее значение, поскольку он указывает на положение нейтральной оси, которая не изменяет длину при изгибе. Обычно коэффициент K находится в диапазоне от 0,3 до 0,5 и зависит от типа материала, толщины, радиуса и метода гибки.
Различные материалы обладают уникальными свойствами, что требует внесения корректировок в расчеты припусков на изгиб. Эти корректировки обеспечивают точность, особенно при изгибах под углом 90°:
Для более мягких материалов, таких как мягкая латунь или медь, припуск на изгиб рассчитывается как:
BA = (0,55 × T) + (1,57 × R
Эта корректировка учитывает пластичность материала и его меньшую устойчивость к деформации.
Для полутвердой меди или латуни, мягкой стали и алюминия припуск на изгиб составляет:
BA = (0,64 x T) + (1,57 × R)
Эти материалы имеют умеренную твердость и требуют несколько большего припуска, чем более мягкие материалы.
Для более твердых материалов, таких как бронза, твердая медь, холоднокатаная сталь и пружинная сталь, формула имеет следующий вид:
BA = (0,71 x T) + (1,57 × R)
Эти материалы более устойчивы к изгибу, что требует большего припуска.
Для определения общей плоской длины детали из листового металла припуск на изгиб добавляется к длине плоских частей:
Плоская длина = Длина ноги 1 + BA + Длина ноги 2
Такой подход обеспечивает точность размеров конечной детали после гибки.
Рассмотрим изгиб на 90° в алюминиевом листе толщиной 2 мм и внутренним радиусом 5 мм. Используйте формулу для полутвердой меди, латуни, мягкой стали и алюминия:
BA = (0,64 × 2) + (1,57 × 5)
BA = 1,28 + 7,85=9,13
Если деталь состоит из двух плоских участков по 50 мм каждый, то общая длина плоского участка составит:
Длина плоской части = 50 + 9,13 + 50 = 109,13 мм
Помимо припусков на изгиб, для точных измерений важны вычеты на изгиб (BD) и внешнее отступление (OSSB):
Вычет на изгиб (BD) = OSSB - BA
Где:
Эти формулировки и соображения необходимы для точного расчета припусков на изгиб, обеспечивая изготовление деталей из листового металла с правильными размерами и посадкой.
Припуск на изгиб - важнейший фактор в процессе гибки листового металла, особенно для таких материалов, как алюминий. Он учитывает растяжение материала, которое происходит во время гибки, обеспечивая точные конечные размеры. Здесь мы обсудим конкретную формулу, используемую для алюминиевых листов, и ее применение.
Припуск на изгиб для алюминиевой пластины можно рассчитать по следующей формуле:
𝐿=𝐿1+𝐿2-1.6𝑇
Где:
Значение 1,6𝑇 получено эмпирическим путем, то есть установлено в результате практических экспериментов и производственного опыта. Этот коэффициент учитывает поведение материала при изгибе, обеспечивая точность конечных размеров.
Важно отметить, что эта формула применима только при определенных условиях:
Чтобы определить расширенный размер алюминиевой пластины, выполните следующие действия:
Этот расчет даст вам длину плоской детали, необходимую перед гибкой, и обеспечит правильные размеры конечной гнутой детали.
Калькулятор припуска на изгиб, представленный ниже, упрощает процесс расчета величины припуска на изгиб, который крайне важен для точного изготовления листового металла. Припуск на изгиб - это длина нейтральной оси между линиями изгиба, которая помогает определить правильный размер заготовки для гнутой детали.
Угол изгиба, обозначаемый как θ, является важнейшим параметром в формуле припуска на изгиб. Он представляет собой угол, на который согнут металлический лист. Угол изгиба обычно измеряется в градусах, но его можно перевести в радианы с помощью формулы:
Внутренний радиус, обозначаемый r, - это радиус внутренней кривой изгиба. Этот радиус напрямую влияет на величину растяжения и сжатия, происходящих в материале при изгибе. Меньший внутренний радиус приводит к более значительной деформации, которая должна быть учтена при расчете припусков на изгиб.
Толщина материала, обозначаемая как T, - это толщина сгибаемого металлического листа. Более толстые материалы испытывают более выраженное растяжение и сжатие, что влияет на общий припуск на изгиб. Точное измерение толщины материала необходимо для точных расчетов припусков на изгиб.
Коэффициент K - это безразмерная величина, которая представляет собой положение нейтральной оси относительно толщины материала. Нейтральная ось - это теоретическая линия внутри материала, длина которой остается неизменной при изгибе. Коэффициент K зависит от свойств материала и методов изгиба, обычно составляя от 0,3 до 0,5 для большинства материалов. Формула для определения положения нейтральной оси выглядит следующим образом:
Нейтральное положение оси = K × T
Нейтральная ось - это воображаемая линия внутри материала, длина которой остается неизменной при изгибе. Понимание ее положения имеет решающее значение для расчета правильного припуска на изгиб.
Припуск на изгиб, обозначаемый как BA, - это длина нейтральной оси, необходимая для формирования изгиба. Она рассчитывается по формуле:
Эта формула использует угол изгиба, внутренний радиус, толщину материала и коэффициент K для обеспечения точных расчетов припусков на изгиб.
Таблица припусков на изгиб - важный ресурс для специалистов, работающих с листовым металлом. Она содержит полный перечень ключевых параметров, таких как толщина материала, радиус изгиба, угол изгиба, припуск на изгиб и значения вычета на изгиб для распространенных материалов. Эта информация очень важна для точного расчета длины развития детали из листового металла после гибки.
Дальнейшее чтение:
| ТЕЛЕВИЗОР | Угол | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Самый короткий размер |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| ТЕЛЕВИЗОР | Угол | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Самый короткий размер |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| Угол | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Самый короткий размер |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| МАТЕРИАЛ | SPCC | SUS | Эл （LY12） | SECC | ||||
|---|---|---|---|---|---|---|---|---|
| T | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
Примечание:
Правильно составленная таблица припусков на гибку - важнейший инструмент в производстве листового металла. Она обеспечивает точность и эффективность процесса гибки, что в конечном итоге приводит к повышению качества и точности готовых изделий. Понимая и используя значения, указанные в таблице, инженеры и изготовители могут добиться оптимальных результатов в своих проектах.
При изготовлении листового металла достижение точности и аккуратности имеет решающее значение для создания высококачественных деталей. Одним из ключевых факторов, играющих значительную роль в этом процессе, является коэффициент K. Понимание коэффициента K и его применение в расчетах припусков на изгиб необходимо изготовителям для производства деталей, которые точно соответствуют техническим условиям и надежно работают в различных отраслях промышленности.
Коэффициент K - это безразмерная величина, представляющая собой отношение расстояния от нейтральной оси к толщине материала. Он имеет решающее значение для точных расчетов припусков на изгиб, которые определяют количество материала, необходимого для достижения желаемого изгиба. Нейтральная ось - это воображаемая линия внутри материала, длина которой не изменяется при изгибе. Понимая коэффициент K, производители могут предсказать, как поведет себя материал при изгибе, обеспечивая точность и эффективность производственных процессов.
Коэффициент K рассчитывается по формуле:
Где:
Использование коэффициента K в формуле припуска на изгиб помогает предсказать удлинение и сжатие материала при изгибе. Формула припуска на изгиб имеет вид:
Чтобы проиллюстрировать это, давайте рассмотрим простой пример. Предположим, у нас есть деталь из листового металла толщиной (T) 2 мм, согнутая под углом 90 градусов (θ), с внутренним радиусом (r) 5 мм и коэффициентом K (K) 0,4.
1. Переведите угол изгиба в радианы:
2. Подставьте полученные значения в формулу припуска на изгиб:
Этот расчет показывает, что для достижения желаемого изгиба вдоль нейтральной оси требуется примерно 9,11 мм материала, что свидетельствует о важности точного коэффициента K.
Коэффициент K напрямую влияет на точность расчетов припусков на изгиб. Точный коэффициент K гарантирует, что окончательные размеры согнутой детали соответствуют проектным спецификациям, что сокращает отходы материала и необходимость доработки. Такая точность жизненно важна для отраслей, где точные размеры имеют решающее значение для сборки и функциональности компонентов.
Различные материалы обладают уникальными механическими свойствами, которые приводят к различным значениям K-Factor. Более мягкие материалы, такие как алюминий, обычно имеют более низкий K-фактор, в то время как более твердые материалы, такие как нержавеющая сталь, имеют более высокий K-фактор. Понимание этих различий позволяет производителям выбирать подходящие значения K-Factor для различных материалов, обеспечивая точность расчетов и эффективность производственных процессов.
Ниже приведены ответы на некоторые часто задаваемые вопросы:
Формула припуска на изгиб используется для расчета длины нейтральной оси изгиба листового металла, что очень важно для определения правильной длины плоской детали перед гибкой металла. Этот расчет гарантирует, что конечные размеры гнутой детали будут соответствовать проектным спецификациям.
Формула учитывает несколько ключевых параметров:
Общая формула припуска на изгиб (BA) выглядит следующим образом:
Используя эту формулу, можно рассчитать точную длину материала, необходимую для формирования изгиба, гарантируя, что материал не будет ни чрезмерно растягиваться, ни слишком сильно сжиматься. Рассчитанный припуск на изгиб затем добавляется к длине ножек детали для получения точного плоского шаблона, который необходим для производства деталей с точными размерами.
Формула припуска на изгиб также связана с вычетом на изгиб, который представляет собой длину, которую необходимо вычесть из общей длины листа для получения правильной плоской детали. Вычет на изгиб рассчитывается с использованием припуска на изгиб и внешнего отступа, что обеспечивает точность конечных размеров детали после гибки.
Например, если вы сгибаете лист нержавеющей стали толщиной 2 мм на угол 90° с внутренним радиусом изгиба 3 мм и коэффициентом K, равным 0,44, припуск на изгиб можно рассчитать следующим образом:
Этот припуск на изгиб используется для правильной разработки плоской детали, в результате чего получается деталь, соответствующая проектным спецификациям. В общем, формула припуска на изгиб необходима для точного изготовления листового металла, обеспечивая производство конечных деталей с правильными размерами.
Чтобы рассчитать припуск на изгиб листового металла, необходимо определить несколько ключевых параметров: толщину материала (T), угол изгиба (θ), внутренний радиус (r) и коэффициент K (K). Припуск на изгиб (BA) рассчитывается по формуле:
Вот пошаговый процесс:
Используя эту формулу, для тех же параметров:
Следуя этим шагам и используя соответствующую формулу, вы сможете точно рассчитать припуск на изгиб для деталей из листового металла, обеспечив точность изготовления.
Коэффициент K важен в формуле припуска на изгиб по нескольким причинам, каждая из которых подчеркивает его значение в точном производстве листового металла. Во-первых, он представляет собой отношение нейтральной оси к толщине материала. Во время изгиба нейтральная ось смещается от своего первоначального положения на 50% толщине материала к внутренней поверхности изгиба. Это смещение очень важно, поскольку оно определяет величину удлинения материала. Коэффициент K помогает рассчитать это новое положение, что необходимо для точных расчетов изгиба.
Во-вторых, коэффициент K является основополагающим при расчете припуска на изгиб, который представляет собой длину нейтрального волокна от начала до конца дуги, образующейся при изгибе. Этот расчет необходим для определения размера плоского листа, требуемого для достижения желаемой формы изгиба. Припуск на изгиб напрямую зависит от коэффициента K, поскольку он учитывает удлинение материала в процессе гибки.
Кроме того, использование коэффициента K позволяет точно рассчитать вычеты на изгиб, внешние отступы и общую плоскую компоновку детали. Такая точность крайне важна, поскольку гарантирует соответствие конечных размеров гнутой детали проектным спецификациям, что позволяет избежать ошибок, которые могут возникнуть при использовании общих или неточных значений коэффициента K.
Коэффициент K зависит от нескольких параметров, включая тип материала, толщину, способ формовки, оснастку и угол изгиба. Такая изменчивость означает, что коэффициент K должен быть адаптирован к конкретным условиям процесса гибки. Учитывая эти факторы, коэффициент K помогает настроить формулу компенсации гибки для достижения более точных результатов.
Наконец, правильное значение коэффициента K необходимо для того, чтобы избежать ошибок в конечных размерах фальцованного листа. Неправильные значения коэффициента K могут привести к неточностям в припусках на изгиб, в результате чего детали не будут соответствовать требуемым техническим характеристикам. Поэтому точное определение и использование коэффициента K имеет решающее значение для производства высококачественных деталей.
В целом, коэффициент K очень важен, поскольку он позволяет точно рассчитать припуски на изгиб, учитывает смещение нейтральной оси, а также специфические параметры материала и процесса - все это необходимо для достижения точных и надежных результатов при гибке листового металла.
Формула припуска на изгиб при гибке листового металла обычно включает несколько ключевых переменных:
Припуск на изгиб (BA) можно рассчитать по формуле:
или
где (0,017453) - (π/180) и (0,0078) - (π /180) x K) - коэффициент.
Эти переменные необходимы для точного определения припуска на изгиб, что очень важно для точного изготовления листового металла.
Да, формула припуска на изгиб может значительно отличаться в зависимости от типа материала, а также других факторов, таких как толщина материала, угол изгиба и конкретный процесс гибки.
Коэффициент K, важнейший компонент формулы припусков на изгиб, представляет собой смещение теоретической нейтральной оси при изгибе и зависит от материала. Например, для низкоуглеродистой холоднокатаной стали обычно используется коэффициент K около 0,446, в то время как другие материалы, такие как нержавеющая сталь и алюминий, имеют другие коэффициенты K из-за их уникальных свойств и поведения при изгибе.
Формула припуска на изгиб также учитывает толщину материала и угол изгиба, которые могут различаться для разных материалов. В общем виде формула припуска на изгиб выглядит следующим образом:
где:
Различные материалы обладают различными свойствами, такими как эластичность, прочность на растяжение и направление зерен, которые влияют на их поведение при изгибе. Например, алюминий гнется легче, чем сталь, что требует корректировки расчета припусков на изгиб. Кроме того, при изгибе металла вдоль направления зерна может потребоваться большее усилие и другой припуск на изгиб по сравнению с изгибом поперек зерна.
Также необходимо учитывать склонность материала к возврату после изгиба, известную как пружинящая спинка. Для этого необходимо слегка перегнуть материал, чтобы учесть упругое восстановление, зависящее от типа материала и его свойств.
В итоге формула припуска на изгиб должна быть подобрана под конкретный используемый материал с учетом его уникальных свойств, толщины и процесса гибки.
Как основатель MachineMFG, я посвятил более десяти лет своей карьеры металлообрабатывающей промышленности. Мой обширный опыт позволил мне стать экспертом в области производства листового металла, механической обработки, машиностроения и станков для обработки металлов. Я постоянно думаю, читаю и пишу об этих предметах, постоянно стремясь оставаться на переднем крае своей области. Позвольте моим знаниям и опыту стать преимуществом для вашего бизнеса.
RU 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT 
PT_BR 
KO 
TR