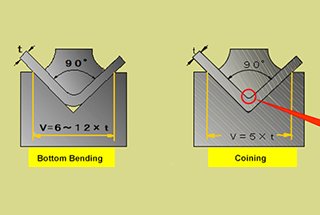
Вы когда-нибудь задумывались, как листовой металл превращается в сложные формы? Ключ к разгадке - вычитание изгиба, важнейшее понятие в производстве листового металла. В этой статье блога мы погрузимся в тонкости вычитания изгиба, изучим его формулы, калькуляторы и практическое применение. Присоединяйтесь к нам, чтобы раскрыть секреты создания точных и красивых деталей из листового металла.
Похожие калькуляторы:
Вычет на изгиб - важнейшее понятие в области производства листового металла, особенно в процессе гибки. Его обычно называют "величиной отступа", и он играет важную роль в определении точных размеров гнутой детали.
Уменьшение на изгиб (BD) - это величина, вычитаемая из общей длины плоского металлического листа для достижения требуемых конечных размеров после гибки. Он учитывает материал, который смещается в процессе гибки.
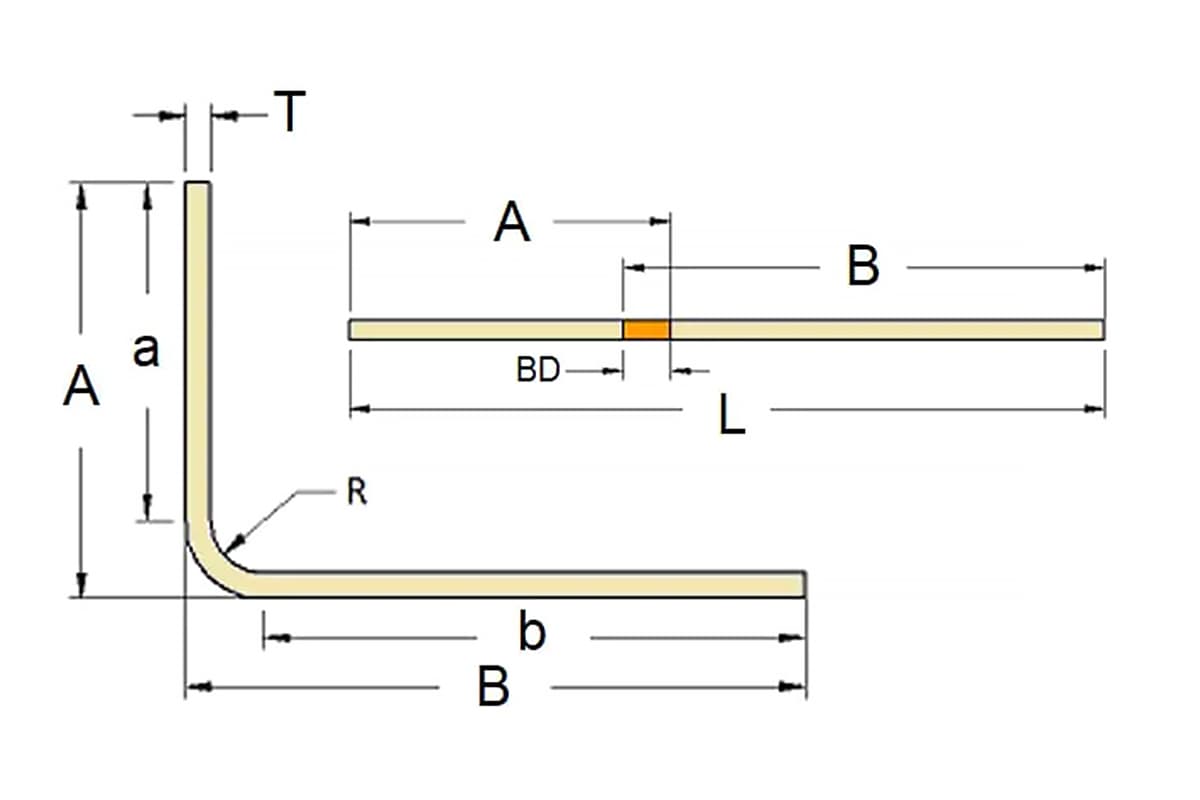
Значение для гибки листового металла
Вычитание изгиба необходимо для точного расчета плоской формы детали из листового металла перед ее гибкой. Это гарантирует, что конечные размеры согнутой детали соответствуют проектным спецификациям. Без учета вычитания изгиба деталь может иметь неправильные размеры, что приведет к потенциальным проблемам при сборке и функциональности.
На величину вычета при сгибе могут влиять несколько факторов, в том числе:
На практике величина вычета на изгиб определяется на основе эмпирических данных, рекомендаций производителя или специализированного программного обеспечения, учитывающего специфические свойства материала и процесс гибки. Точные расчеты вычетов на изгиб имеют решающее значение для обеспечения соответствия конечного продукта требованиям конструкции и его правильного функционирования в предполагаемом применении.
Вычет на изгиб (BD) - это критический фактор при изготовлении листового металла, используемый для расчета длины плоской детали из листового металла. Он учитывает материал, который смещается в процессе гибки. Эта величина необходима для обеспечения точности конечных размеров гнутой детали.
Формула вычитания изгиба используется для определения плоской длины детали из листового металла перед ее сгибанием. Формула выглядит следующим образом:
Lt=A+B-BD
Где:
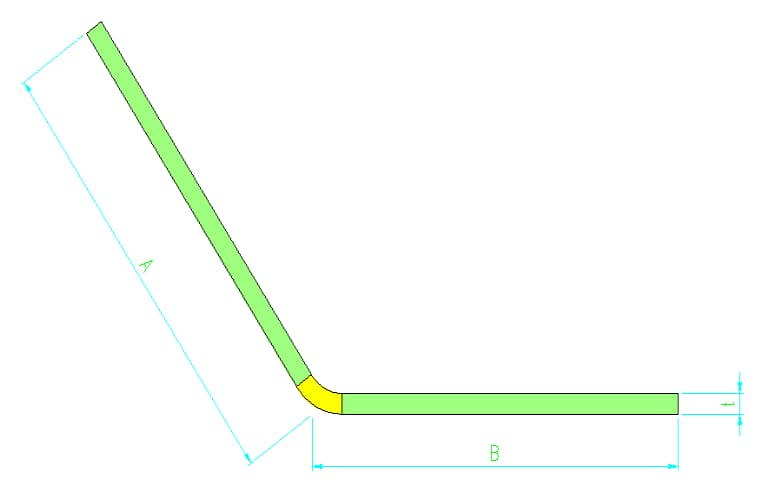
Вычет на изгиб в Solidworks используется только для расчета 90-градусных изгибов в листовом металле.
Однако его можно использовать и для расчета разгибания листового металла на угол не 90 градусов, но при этом необходимо использовать значение вычета на изгиб при изгибе на угол не 90 градусов в соответствии с таблицей коэффициентов изгиба.
У каждого производителя своя таблица, и в ней могут быть ошибки. Некоторые заводы по производству листового металла могут не часто использовать гибки под углом не 90 градусов.
Сегодня я расскажу об известном мне методе расчета вычета при изгибе под углом 90 градусов.
Выдержка при изгибе является решающим фактором при изготовлении листового металла, особенно при использовании таких станков, как листогибочные прессы. Она представляет собой количество материала, израсходованного в процессе гибки. Точный расчет отчислений на гибку необходим для получения точных размеров детали и эффективного использования материала. В этой статье рассматриваются три распространенных метода расчета отчислений на гибку.
В самом простом методе используется коэффициент умножения, основанный на толщине материала:
Этот метод быстр и прост, но не обладает достаточной точностью. Он подходит для приложений с невысокими требованиями к точности или для первоначальных оценок.
Более тонкий подход, разработанный промышленностью листового металла:
Вычет на изгиб = 2 × толщина материала + 1/3 × толщина материала
Эта формула учитывает удлинение материала при изгибе. Она выводится следующим образом: длина в развернутом виде = длина A + длина B - вычет на изгиб
При вычете на изгиб учитывается как толщина материала, так и его удлинение.
Более сложная формула, полученная на основе эмпирических исследований:
Вычет на изгиб = 2 × t - (0,72t - 0,075V - 0,01)
Где:
Эта формула учитывает влияние меньшей ширины штампа на вычет при гибке. Она особенно точна для листов из углеродистой стали, но показала хорошие результаты и для других материалов, например алюминия, когда ширина штампа примерно в 4 раза больше толщины материала.
Важные соображения
Заключение
Выбор подходящего метода расчета вычета на изгиб зависит от требуемой точности, типа материала и имеющейся информации об оснастке. Для высокоточных работ рекомендуется использовать усовершенствованную формулу (метод 3), в то время как более простые методы могут быть полезны для быстрых расчетов или менее ответственных задач.
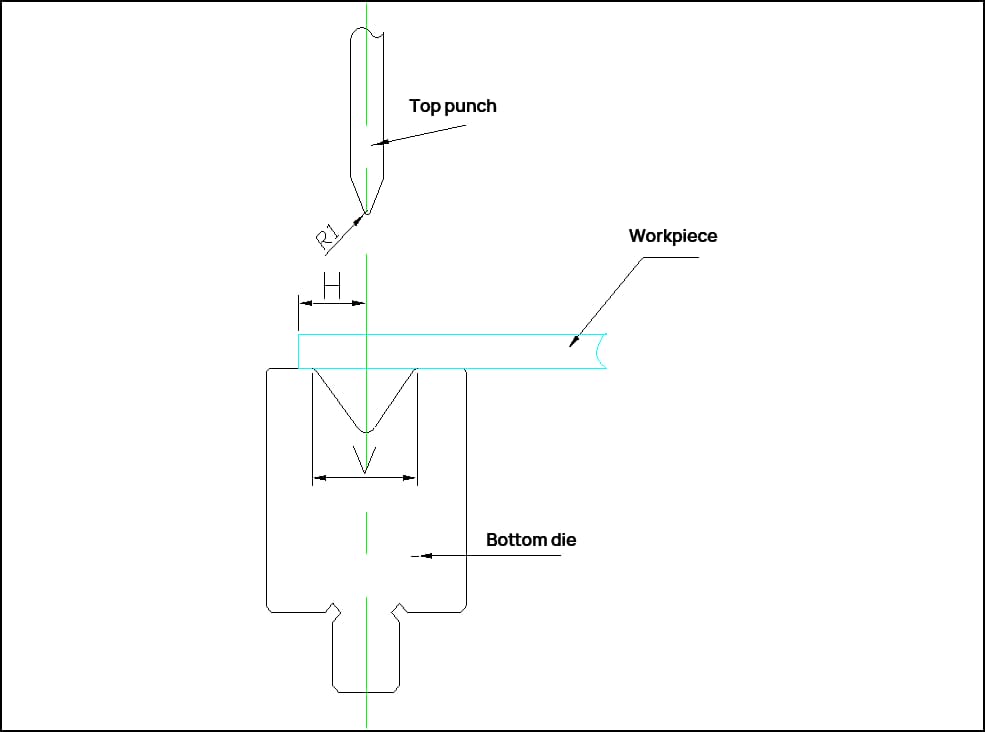
| V | Ширина матрицы w | Радиус изгиба | T | 30° | 45° | 60° | 90° | 120° | 150° | 180° | Внешний слой с двойным изгибом 90° | Минимальный размер изгиба H | Минимальный размер Z-образного изгиба (Z) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8.0 | 12.0 | R1 | 0.6 | 0.2 | 0.5 | 0.9 | 1.0 | 0.7 | 0.2 | 0.3 | 1.9 | 6.0 | 10.0 |
| 0.8 | 0.3 | 0.6 | 1.0 | 1.6 | 0.8 | 0.3 | 0.4 | 2.2 | |||||
| 1 | 0.3 | 0.7 | 1.1 | 1.7 | 0.9 | 0.3 | 0.5 | 2.5 | |||||
| 1.2 | 0.4 | 0.8 | 1.3 | 2.2 | 1.1 | 0.4 | 0.6 | 2.8 | |||||
| R2 | 0.6 | 0.2 | 0.5 | 0.9 | 1.6 | 0.7 | 0.2 | 0.3 | 1.9 | ||||
| 0.8 | 0.3 | 0.6 | 1.2 | 1.8 | 0.8 | 0.3 | 0.4 | 2.2 | |||||
| 1 | 0.3 | 0.7 | 1.2 | 2.0 | 0.9 | 0.3 | 0.5 | 2.5 | |||||
| 1.2 | 0.4 | 0.8 | 1.4 | 2.3 | 1.1 | 0.4 | 0.6 | 2.8 | |||||
| 10.0 | 14.0 | R1 | 1.5 | 0.7 | 1.2 | 1.6 | 2.5 | 1.3 | 0.5 | 0.7 | 3.2 | 7.0 | 11.0 |
| R2 | 1.5 | 0.6 | 1.0 | 1.5 | 2.7 | 1.3 | 0.5 | 0.7 | 3.5 | ||||
| 12.0 | 16.0 | R1 | 2 | 0.6 | 1.3 | 2.0 | 3.4 | 1.7 | 0.6 | 0.9 | 4.4 | 8.5 | 13.0 |
| R2 | 2 | 0.9 | 1.4 | 2.0 | 3.6 | 1.7 | 0.6 | 0.9 | 4.5 | ||||
| 16.0 | 26.0 | R1 | 2.5 | 0.7 | 1.5 | 2.4 | 4.3 | 2.2 | 0.8 | 1.1 | 5.6 | 12.0 | 20.0 |
| 3 | 0.8 | 1.7 | 2.8 | 5.1 | 2.8 | 0.8 | 1.3 | 5.8 | |||||
| R2 | 2.5 | 0.8 | 1.6 | 2.5 | 4.8 | 2.3 | 0.9 | 1.1 | 6.2 | ||||
| 3 | 1.0 | 2.0 | 3.0 | 5.2 | 2.8 | 1.0 | 1.3 | 6.4 | |||||
| 22.0 | 32.5 | R1 | 4 | 1.0 | 2.4 | 3.5 | 6.5 | 3.3 | 1.1 | 16.0 | 26.0 | ||
| R2 | 4 | 1.2 | 2.6 | 4.0 | 6.8 | 3.5 | 1.1 | ||||||
| 32.0 | 50.0 | R1 | 5 | 1.2 | 3.2 | 4.8 | 8.6 | 4.6 | 1.4 | 24.0 | 38.0 | ||
| 6 | 1.5 | 3.5 | 4.5 | 9.5 | 5.0 | 1.8 | |||||||
| R2 | 5 | 1.5 | 3.4 | 5.0 | 8.8 | 4.5 | 1.6 | ||||||
| 6 | 1.8 | 3.8 | 5.5 | 9.8 | 5.2 | 2.0 |
Объяснение:
| Формула | 0.2t | 0.4t | 0.6t | 0.8t | 1.0t | 1.2t | 1.4t | 1.6t |
| Угол | 155-165° | 145-155° | 135-145° | 125-135° | 115-125° | 105-115° | 95-105° | 85-95° |
| Толщина (t) | 15-25° | 25-35° | 35-45° | 45-55° | 55-65° | 65-75° | 75-85° | |
| 0.5 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 |
| 0.6 | 0.12 | 0.24 | 0.36 | 0.48 | 0.60 | 0.72 | 0.84 | 0.96 |
| 0.8 | 0.16 | 0.32 | 0.48 | 0.64 | 0.80 | 0.96 | 1.12 | 1.28 |
| 1.0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 |
| 1.2 | 0.24 | 0.48 | 0.72 | 0.96 | 1.20 | 1.44 | 1.68 | 1.92 |
| 1.5 | 0.30 | 0.60 | 0.90 | 1.20 | 1.50 | 1.80 | 2.10 | 2.40 |
| 2.0 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 | 3.20 |
| 2.5 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 | 4.00 |
| 3.0 | 0.60 | 1.20 | 1.80 | 2.40 | 3.00 | 3.60 | 4.20 | 4.80 |
| 4.0 | 0.80 | 1.60 | 2.40 | 3.20 | 4.00 | 4.80 | 5.60 | 6.40 |
| 4.5 | 0.90 | 1.80 | 2.70 | 3.60 | 4.50 | 5.40 | 6.30 | 7.20 |
| 5.0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.00 | 8.00 |
| 6.0 | 1.20 | 2.40 | 3.60 | 4.80 | 6.00 | 7.20 | 8.40 | 9.60 |
| Формула | 0.3t | 0.5t | 0.7t | 0.9t | 1.1t | 1.3t | 1.5t | 1.7t |
| Угол | 155-165° | 145-155° | 135-145° | 125-135° | 115-125° | 105-115° | 95-105° | 85-95° |
| Толщина (t) | 15-25° | 25-35° | 35-45° | 45-55° | 55-65° | 65-75° | 75-85° | |
| 0.5 | 0.15 | 0.25 | 0.35 | 0.45 | 0.55 | 0.65 | 0.75 | 0.85 |
| 0.6 | 0.18 | 0.30 | 0.42 | 0.54 | 0.66 | 0.78 | 0.90 | 1.02 |
| 0.8 | 0.24 | 0.40 | 0.56 | 0.72 | 0.88 | 1.04 | 1.20 | 1.36 |
| 1.0 | 0.30 | 0.50 | 0.70 | 0.90 | 1.10 | 1.30 | 1.50 | 1.70 |
| 1.2 | 0.36 | 0.60 | 0.84 | 1.08 | 1.32 | 1.56 | 1.80 | 2.04 |
| 1.5 | 0.45 | 0.75 | 1.05 | 1.35 | 1.65 | 1.95 | 2.25 | 2.55 |
| 2.0 | 0.60 | 1.00 | 1.40 | 1.80 | 2.20 | 2.60 | 3.00 | 3.40 |
| 2.5 | 0.75 | 1.25 | 1.75 | 2.25 | 2.75 | 3.25 | 3.75 | 4.25 |
| 3.0 | 0.90 | 1.50 | 2.10 | 2.70 | 3.30 | 3.90 | 4.50 | 5.10 |
| 4.0 | 1.20 | 2.00 | 2.80 | 3.60 | 4.40 | 5.20 | 6.00 | 6.80 |
| 4.5 | 1.35 | 2.25 | 3.15 | 4.05 | 4.95 | 5.85 | 6.75 | 7.65 |
| 5.0 | 1.50 | 2.50 | 3.50 | 4.50 | 5.50 | 6.50 | 7.50 | 8.50 |
| 6.0 | 1.80 | 3.00 | 4.20 | 5.40 | 6.60 | 7.80 | 9.00 | 10.20 |
| Нет. | Угол / Толщина | 0.8 | 1.0 | 1.2 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 5.0 |
| 1 | 0 | 3.00 | 3.60 | 4.00 | 5.00 | 7.00 | 8.40 | 10.00 | 14.00 | 20.00 |
| 2 | 5 | 2.92 | 3.50 | 3.89 | 4.86 | 6.81 | 8.17 | 9.72 | 13.61 | 19.44 |
| 3 | 10 | 2.83 | 3.40 | 3.78 | 4.72 | 6.61 | 7.93 | 9.44 | 13.22 | 18.89 |
| 4 | 15 | 2.75 | 3.30 | 3.67 | 4.58 | 6.42 | 7.70 | 9.17 | 12.83 | 18.33 |
| 5 | 20 | 2.67 | 3.20 | 3.56 | 4.44 | 6.22 | 7.47 | 8.89 | 12.44 | 17.78 |
| 6 | 25 | 2.58 | 3.10 | 3.44 | 4.31 | 6.03 | 7.23 | 8.61 | 12.06 | 17.22 |
| 7 | 30 | 2.50 | 3.00 | 3.33 | 4.17 | 5.83 | 7.00 | 8.33 | 11.67 | 16.67 |
| 8 | 35 | 2.42 | 2.90 | 3.22 | 4.03 | 5.64 | 6.77 | 8.06 | 11.28 | 16.11 |
| 9 | 40 | 2.33 | 2.80 | 3.11 | 3.89 | 5.44 | 6.53 | 7.78 | 10.89 | 15.56 |
| 10 | 45 | 2.25 | 2.70 | 3.00 | 3.75 | 5.25 | 6.30 | 7.50 | 10.50 | 15.00 |
| 11 | 50 | 2.17 | 2.60 | 2.89 | 3.61 | 5.06 | 6.07 | 7.22 | 10.11 | 14.44 |
| 12 | 55 | 2.08 | 2.50 | 2.78 | 3.47 | 4.86 | 5.83 | 6.94 | 9.72 | 13.89 |
| 13 | 60 | 2.00 | 2.40 | 2.67 | 3.33 | 4.67 | 5.60 | 6.67 | 9.33 | 13.33 |
| 14 | 65 | 1.92 | 2.30 | 2.56 | 3.19 | 4.47 | 5.37 | 6.39 | 8.94 | 12.78 |
| 15 | 70 | 1.83 | 2.20 | 2.44 | 3.06 | 4.28 | 5.13 | 6.11 | 8.56 | 12.22 |
| 16 | 75 | 1.75 | 2.10 | 2.33 | 2.92 | 4.08 | 4.90 | 5.83 | 8.17 | 11.67 |
| 17 | 80 | 1.67 | 2.00 | 2.22 | 2.78 | 3.89 | 4.67 | 5.56 | 7.78 | 11.11 |
| 18 | 85 | 1.58 | 1.90 | 2.11 | 2.64 | 3.69 | 4.43 | 5.28 | 7.39 | 10.56 |
| 19 | 90 | 1.50 | 1.80 | 2.00 | 2.50 | 3.50 | 4.20 | 5.00 | 7.00 | 10.00 |
| 20 | 95 | 1.42 | 1.70 | 1.89 | 2.36 | 3.31 | 3.97 | 4.72 | 6.61 | 9.44 |
| 21 | 100 | 1.33 | 1.60 | 1.78 | 2.22 | 3.11 | 3.73 | 4.44 | 6.22 | 8.89 |
| 22 | 105 | 1.25 | 1.50 | 1.67 | 2.08 | 2.92 | 3.50 | 4.17 | 5.83 | 8.33 |
| 23 | 110 | 1.17 | 1.40 | 1.56 | 1.94 | 2.72 | 3.27 | 3.89 | 5.44 | 7.78 |
| 24 | 115 | 1.08 | 1.30 | 1.44 | 1.81 | 2.53 | 3.03 | 3.61 | 5.06 | 7.22 |
| 25 | 120 | 1.00 | 1.20 | 1.33 | 1.67 | 2.33 | 2.80 | 3.33 | 4.67 | 6.67 |
| 26 | 125 | 0.92 | 1.10 | 1.22 | 1.53 | 2.14 | 2.57 | 3.06 | 4.28 | 6.11 |
| 27 | 130 | 0.83 | 1.00 | 1.11 | 1.39 | 1.94 | 2.33 | 2.78 | 3.89 | 5.56 |
| 28 | 135 | 0.75 | 0.90 | 1.00 | 1.25 | 1.75 | 2.10 | 2.50 | 3.50 | 5.00 |
| 29 | 140 | 0.67 | 0.80 | 0.89 | 1.11 | 1.56 | 1.87 | 2.22 | 3.11 | 4.44 |
| 30 | 145 | 0.58 | 0.70 | 0.78 | 0.97 | 1.36 | 1.63 | 1.94 | 2.72 | 3.89 |
| 31 | 150 | 0.50 | 0.60 | 0.67 | 0.83 | 1.17 | 1.40 | 1.67 | 2.33 | 3.33 |
| 32 | 155 | 0.42 | 0.50 | 0.56 | 0.69 | 0.97 | 1.17 | 1.39 | 1.94 | 2.78 |
| 33 | 160 | 0.33 | 0.40 | 0.44 | 0.56 | 0.78 | 0.93 | 1.11 | 1.56 | 2.22 |
| 34 | 165 | 0.25 | 0.30 | 0.33 | 0.42 | 0.58 | 0.70 | 0.83 | 1.17 | 1.67 |
| 35 | 170 | 0.17 | 0.20 | 0.22 | 0.28 | 0.39 | 0.47 | 0.56 | 0.78 | 1.11 |
| 36 | 175 | 0.08 | 0.10 | 0.11 | 0.14 | 0.19 | 0.23 | 0.28 | 0.39 | 0.56 |
| 37 | 180 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
1) Таблица вычетов при гибке применяется для процессов гибки листового металла, когда не используется прижимная плита, а ширина листа превышает толщину (t) более чем в три раза.
2) При гибке на гибочном станке расчеты можно производить в соответствии с этой таблицей.
3) В соответствии с размерами, указанными на диаграмме, формула расчета развернутого размера гнутой заготовки выглядит следующим образом:
L=a+b-y
Где:
4) В связи с многочисленными факторами, влияющими на гибку листового металла, данная таблица значений вычетов при гибке листового металла приведена только для справки.
Точность размеров гнутых заготовок зависит от точности позиционирования заднего калибра листогибочного пресса и точности листа. металлорежущий станок. Использование надежных станков как для резки, так и для гибки позволяет решить эти проблемы.
Критическим фактором, влияющим на точность размеров гнутых заготовок, является точность разработки плоского шаблона листа. Когда плоский лист сгибается в заготовку с определенным углом, измерение размеров согнутой заготовки показывает, что они не равны размерам плоского листа, как показано на рисунке.
Это расхождение известно как "вычет на изгиб".
Если вычеты при гибке неточны, размер плоской детали будет неточным, и независимо от точности последующих операций конечная заготовка не будет соответствовать требуемой точности размеров.
Вычеты при изгибе сложны, и простейший метод заключается в том, чтобы просто использовать удвоенную толщину материала.
Однако такой подход довольно груб. Более точным методом является применение теории нейтральной оси из стандарта DIN 6935, которая предполагает вычисление коэффициента "k" и его сочетание с толщиной и углом сгибаемого листа.
Эта формула дает более точный расчет на изгиб. Однако даже вычеты на изгиб, рассчитанные по теории нейтральной оси из DIN 6935, могут быть недостаточно точными, поскольку фактические вычеты зависят также от характеристик материала, толщины и угол изгиба, а также используемые инструменты.
Различные материалы, толщины и методы расчета дают разную величину отчислений на изгиб, как показано в таблице ниже.
Таблица Величина вычитания для размеров изгиба, соответствующих различным материалам, толщинам и методам
| Толщина листа S/мм | Die | Материал | -S × 2 | DIN6935 | База данных |
| 1.5 | V12/78 | DC04 | -3.00 | -3.00 | -2.90 |
| 1.5 | V08/78 | DC04 | -3.00 | -2.80 | -2.70 |
| 1.5 | V1278 | X5CrNi1810 | -3.00 | -3.00 | -3.10 |
| 4 | V24/78 | S235JRG2 | -8.00 | -7.60 | -7.09 |
| 4 | V30/78 | S235JRG2 | -8.00 | -7.57 | -7.26 |
| 4 | V24/78 | X5CrNi1810 | -8.00 | -8.01 | -7.57 |
| 4 | V30/78 | X5CrNi1810 | -8.00 | -7.90 | -8.01 |
| 6 | V30/78 | S235JRG2 | -12.00 | -11.20 | -10.35 |
| 6 | V4078 | S235JRG2 | -12.00 | -11.60 | -10.62 |
| 6 | V30/78 | X5CrNi1810 | -12.00 | -11.20 | -10.89 |
| 6 | V4078 | X5CrNi1810 | -12.00 | -11.60 | -11.60 |
Например, для листа S235JRG2 толщиной 4 мм при использовании нижнего штампа V30 вычет на изгиб зависит от метода: удвоенная толщина материала дает 8 мм, формула DIN 6935 - 7,57 мм, а эмпирическое значение из базы данных - 7,26 мм.
Между методами существуют расхождения, которые становятся еще более значительными, когда заготовки требуют нескольких изгибов, что приводит к большим суммарным отклонениям. Эмпирические значения из базы данных получены в результате обширных практических испытаний и хранятся в базе данных, обеспечивая максимальную точность.
Как основатель MachineMFG, я посвятил более десяти лет своей карьеры металлообрабатывающей промышленности. Мой обширный опыт позволил мне стать экспертом в области производства листового металла, механической обработки, машиностроения и станков для обработки металлов. Я постоянно думаю, читаю и пишу об этих предметах, постоянно стремясь оставаться на переднем крае своей области. Позвольте моим знаниям и опыту стать преимуществом для вашего бизнеса.
RU 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
KO