Руководство для экспертов по расчету напряжений сдвига при изгибе и прочности балок

На поперечное сечение балки, находящейся под действием поперечной силы, действуют как изгибающий момент, так и сдвигающая сила, в результате чего в поперечном сечении возникают как нормальные напряжения, так и напряжения сдвига. Далее будут рассмотрены напряжения сдвига при изгибе для нескольких распространенных сечений балки.

Прямоугольное сечение

Небольшой отрезок длиной dx отрезается от балки под действием поперечной силы изгиба. Балка не имеет нагрузки, а сдвигающие силы с обеих сторон отрезка равны, но направлены в противоположные стороны. Изгибающий момент на правом участке больше, чем на левом, в результате чего нормальные напряжения на этих двух участках различны.

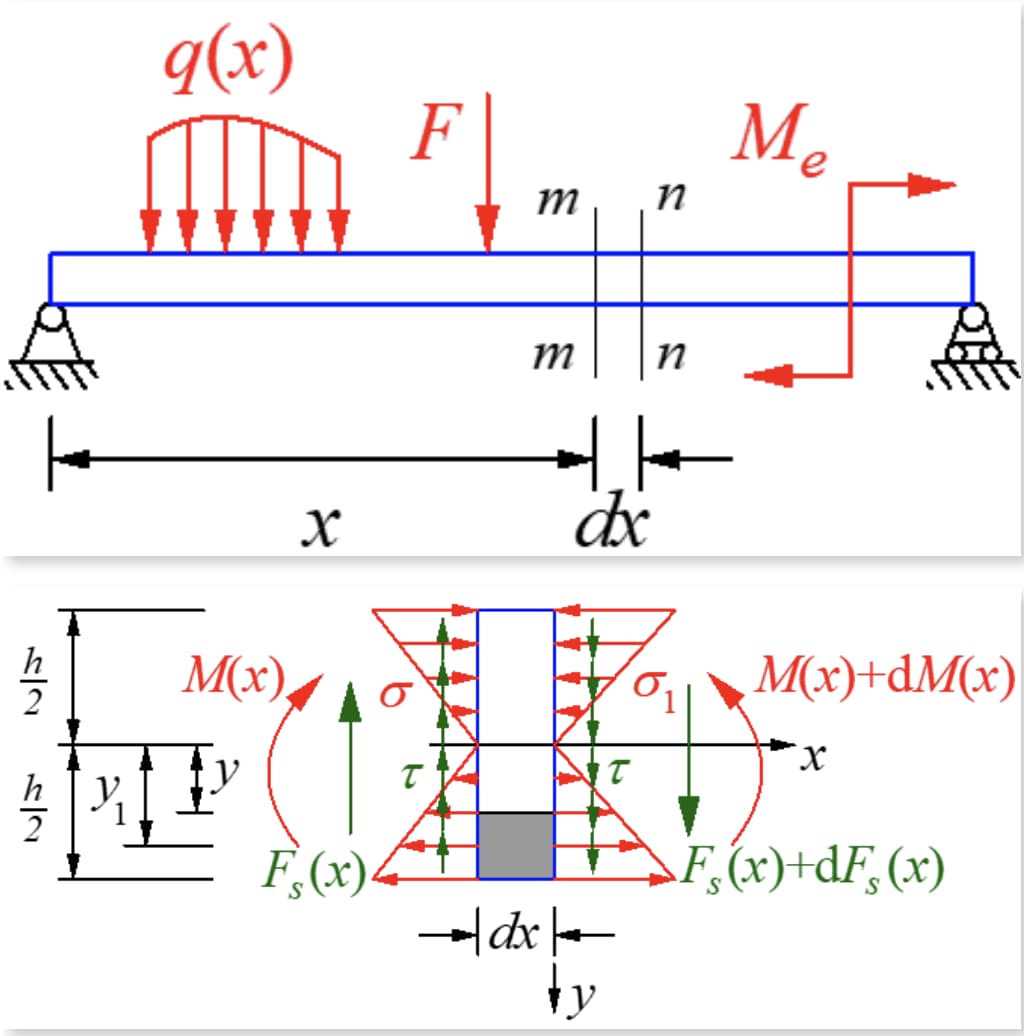
Для узкого прямоугольного сечения напряжение сдвига направлено по касательной к границе с обеих сторон балки из-за отсутствия напряжения сдвига на стороне. Это означает, что, поскольку балка симметрично изогнута и параллельна границе, напряжение сдвига на оси симметрии должно быть в направлении y и мало изменяться вдоль направления ширины.

Поэтому для закона распределения напряжения сдвига по поперечному сечению делаются следующие предположения:

• Направление сдвигающего напряжения в каждой точке поперечного сечения параллельно сдвигающей силе;
• Напряжение сдвига равномерно распределено по ширине секции, то есть напряжение сдвига в каждой точке на горизонтальной линии, параллельной нейтральной оси, одинаково.

Когда отношение высоты к ширине сечения больше 2, решение, основанное на вышеприведенном предположении, достаточно точно по сравнению с точным решением из теории упругости.

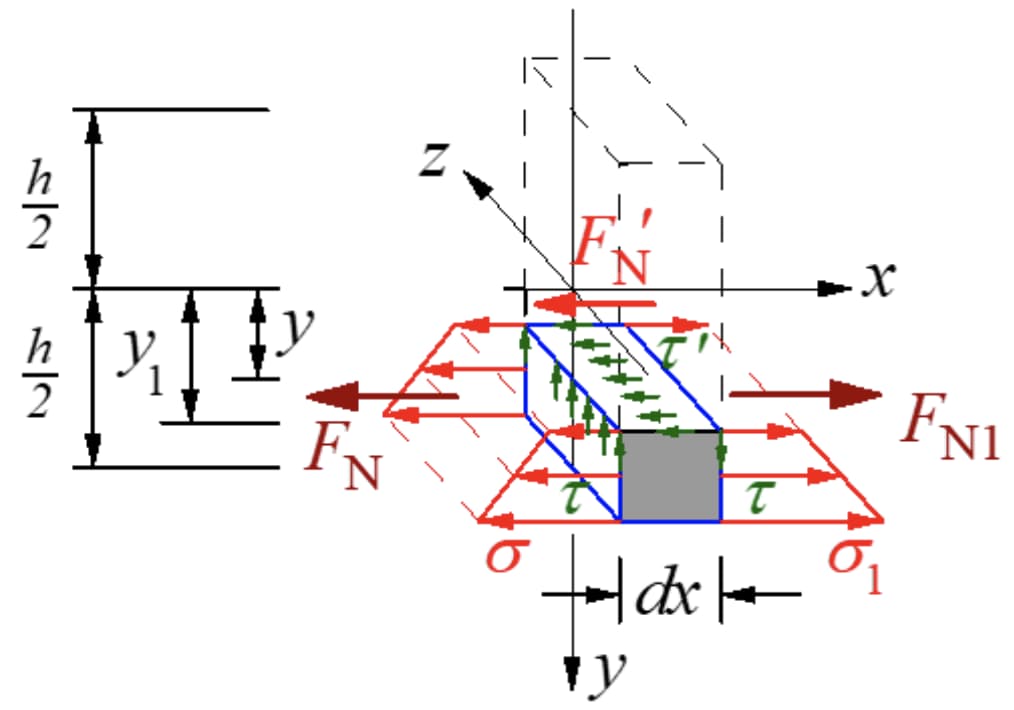
Согласно теореме о взаимности напряжений сдвига, на продольном участке, перпендикулярном поперечному сечению, должно быть напряжение сдвига, равное размеру поперечного сечения. Вырежьте микросегмент вдоль продольной плоскости с нейтральной осью момента в направлении от y и возьмите микроэлемент на нижней стороне продольной плоскости. Усилия будут такими, как показано на рисунке ниже.

Результирующая сила нормального напряжения на левом участке равна:

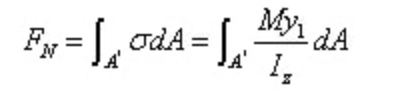
Результирующая сила нормального напряжения на правом участке равна：

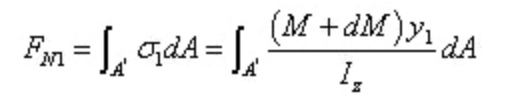
Очевидно, что два результирующих элемента имеют разные размеры. Для поддержания равновесия микросегмента на продольном сечении должна действовать сила, направленная вдоль осевого направления. Эта сила является результатом напряжения сдвига, что подтверждает наличие напряжения сдвига на продольном сечении.

Поскольку dx мало, пусть напряжение сдвига в продольной плоскости распределено равномерно：.

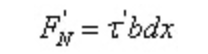
В соответствии с условиями равновесия：

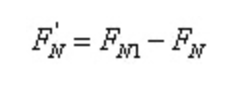
Это,

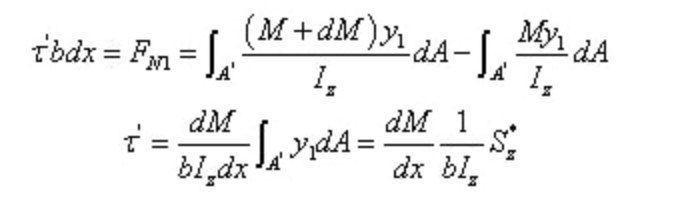
Среди,

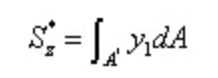
Из теоремы о взаимности напряжений сдвига и дифференциальной зависимости между сдвигающей силой и изгибающим моментом:

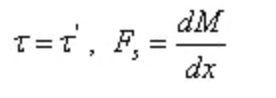
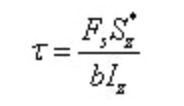
Из них:

• b - ширина горизонтальной линии с нейтральной осью момента y на сечении, которая постоянна для прямоугольных сечений;
• I_z момент инерции нейтральной оси всего сечения;
• S_z* статический момент участка вне горизонтальной линии, нейтральная ось которой проходит через ось y в поперечном сечении к нейтральной оси;
• F_S сила сдвига в поперечном сечении.

Среди,

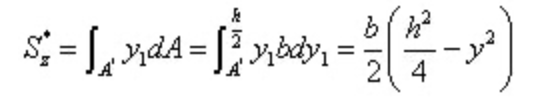
Подставьте в формулу расчета напряжения сдвига

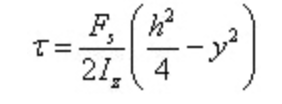
Напряжение сдвига распределено по параболе по высоте сечения.

При y=0 максимальное напряжение сдвига в сечении на нейтральной оси

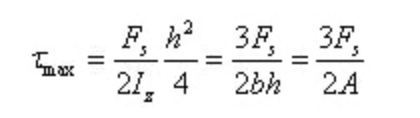
Угловая деформация - это

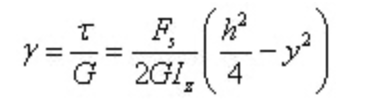
Видно, что угловая деформация также распределена по параболе по высоте сечения.

В это время форма искривления поперечного сечения при изгибе поперечной силы показана на рисунке ниже, что подтверждает, что деформация при изгибе поперечной силы не соответствует предположению о плоскости.

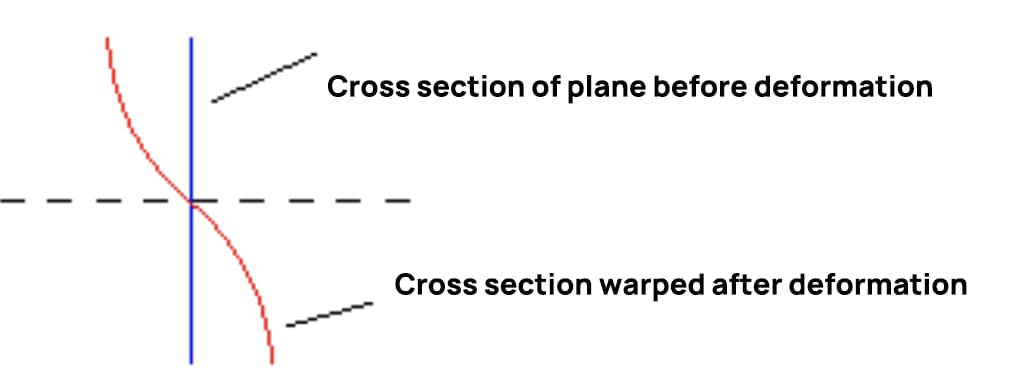
Когда сила сдвига остается постоянной, напряжение сдвига на последовательных поперечных сечениях одинаково, и степень искривления также одинакова. Длина продольных волокон не изменяется из-за искривления сечения, поэтому это не приводит к возникновению дополнительных нормальных напряжений. Если сдвигающая сила изменяется в зависимости от положения сечения, степень искривления двух последовательных сечений будет разной, что приведет к появлению дополнительных нормальных напряжений в сечении.

Для симметричных сечений другой формы приближенное решение по напряжению сдвига может быть получено с помощью описанного выше метода.

Для прямоугольного сечения в формуле расчета напряжений ширина сечения (b) постоянна, а статический момент половины площади сечения по одну сторону от нейтральной оси к нейтральной оси наибольший. В результате напряжение сдвига в каждой точке на нейтральной оси будет наибольшим.

Для симметричных сечений других форм максимальное напряжение сдвига в поперечном сечении обычно находится в различных точках на нейтральной оси, за исключением сечений со значительно увеличенной шириной на нейтральной оси (например, поперечных сечений) или некоторых сечений с переменной шириной (например, сечений в виде равнобедренного треугольника).

Поэтому для балок I-образного, кольцевого и круглого сечения ниже будет рассмотрено в основном максимальное напряжение сдвига в каждой точке на нейтральной оси.

Круглое сечение

Напряжение сдвига в каждой точке края кругового сечения направлено по касательной к окружности в соответствии с теоремой о взаимном напряжении сдвига. В каждой точке оси симметрии напряжение сдвига должно быть в направлении y. Можно считать, что распределение напряжения сдвига сходится в точке на оси симметрии для каждой точки по ширине y от нейтральной оси, а компоненты напряжения сдвига вдоль направления Y в каждой точке по ширине равны.

Максимальное напряжение сдвига кругового сечения по-прежнему находится на нейтральной оси, а его направление параллельно внешней силе, причем в каждой точке нейтральной оси оно имеет одно и то же значение.

Максимальное напряжение сдвига составляет

I-образное сечение

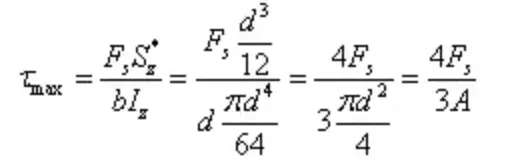
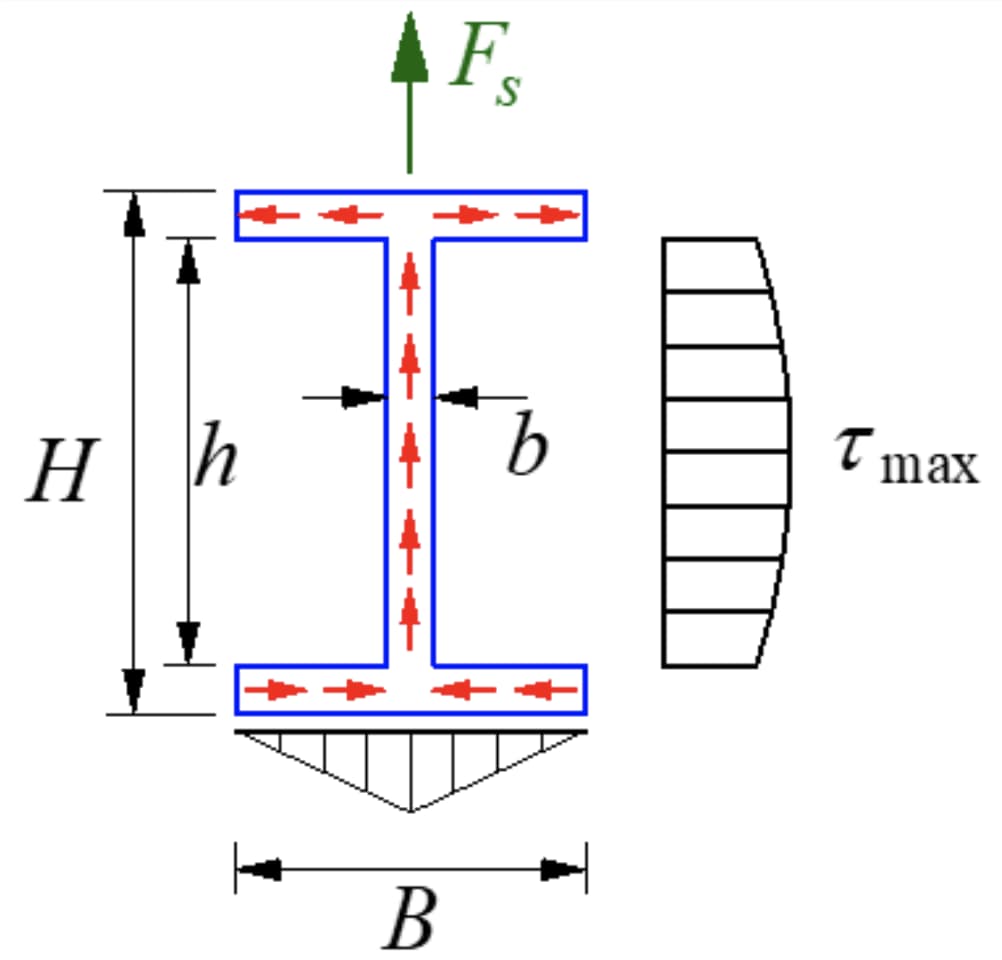
I-образное сечение представляет собой тонкостенное открытое сечение с распределением напряжений, как показано на рисунке. Величина сдвигающего напряжения по толщине стенки одинакова, что называется потоком сдвигающих напряжений, текущим в направлении сдвига.

Компонента напряжения сдвига, параллельная оси y на фланце, является второстепенной и незначительной, основное внимание уделяется компоненте, параллельной длинной стороне фланца. Напряжение сдвига на полотне имеет параболическое распределение, размер которого показан на рисунке.

Максимальное напряжение сдвига приходится на нейтральную ось.

В случае I-образная стальмаксимальное напряжение сдвига:

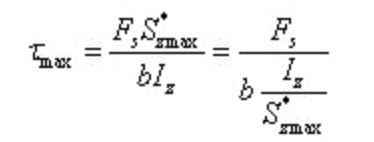
Где b - толщина полотна, а I_z/s*_zmax можно получить, обратившись к таблице профильной стали.

Если это I-образное сечение, состоящее из трех длинных и узких прямоугольников, то максимальные и минимальные напряжения сдвига на полотне можно получить следующим образом:

Из приведенных выше двух формул видно, что ширина полотна намного меньше ширины фланца, поэтому максимальное напряжение сдвига на полотне не сильно отличается от минимального напряжения сдвига.

Поэтому можно считать, что напряжение сдвига на полотне распределено примерно равномерно.

Результирующее напряжение сдвига на полотне составляет 95-97% от общей сдвигающей силы, а сдвигающая сила на поперечном сечении в основном воспринимается полотном.

Поскольку на полотно приходится почти вся сдвигающая сила, а сдвигающее напряжение на полотне распределено почти равномерно, максимальное сдвигающее напряжение можно приблизительно рассчитать, разделив сдвигающую силу на площадь поперечного сечения брюшного столба:

В то же время вся территория Двутавровая балка Фланец находится дальше всего от нейтральной оси, и нормальное напряжение в каждой точке относительно велико, поэтому фланец принимает на себя большую часть изгибающего момента, действующего на сечение.

Тонкостенная кольцевая секция

Толщина тонкостенного кольцевого сечения равна d, средний радиус кольца равен r, а толщина намного меньше среднего радиуса, поэтому можно предположить, что:

Напряжение сдвига в поперечном сечении одинаково по толщине стенки;

Направление сдвигающего напряжения направлено по касательной к центральной линии сечения, а направление потока сдвигающего напряжения - вдоль направления сдвига.

Максимальное напряжение сдвига расположено на нейтральной оси:

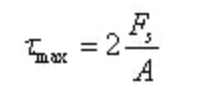
Где A - площадь кольцевого сечения.

Состояние прочности балки

Нормальная прочность при изгибе:

Для нейтральных осесимметричных сечений максимальное растягивающее нормальное напряжение и максимальное сжимающее нормальное напряжение равны.

Обычно используются пластиковые материалы и условия их прочности:

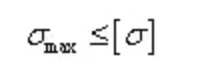
Для сечения с несимметричной нейтральной осью максимальное растягивающее нормальное напряжение и максимальное сжимающее нормальное напряжение не равны.

Обычно используются хрупкие материалы и условия их прочности:

Условием прочности при изгибе является напряжение сдвига:

Меры по повышению прочности балок на изгиб

Изгибающее нормальное напряжение является основным фактором, управляющим балкой.

Поэтому условие прочности по нормальным напряжениям при изгибе часто является основной базой для проектирования балок.

Исходя из условий прочности, для улучшения несущей способности балки следует рассмотреть два аспекта:

С одной стороны, нагрузка на балку должна быть разумной, чтобы уменьшить максимальный изгибающий момент;

С другой стороны, для улучшения коэффициента сечения при изгибе и полного использования свойств материала принята разумная форма сечения.

1. Разумно расположить напряжение в балке

Улучшите напряженное состояние балки и постарайтесь уменьшить максимальный изгибающий момент в балке.

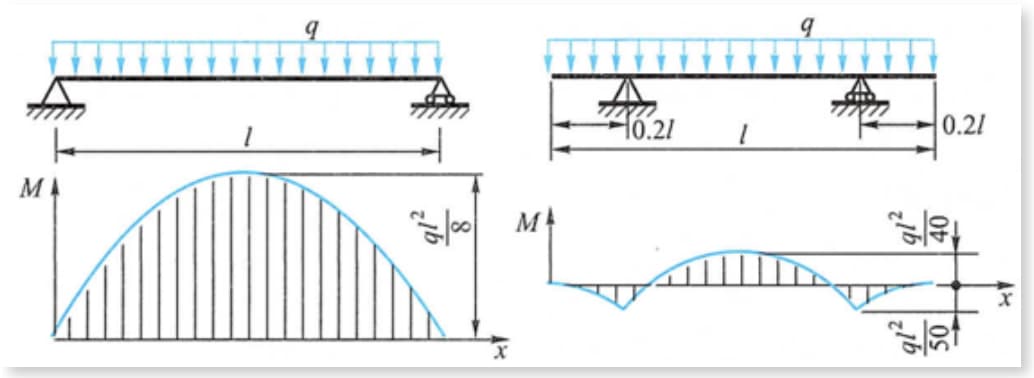
Как показано на рис., максимальный изгибающий момент на балке при равномерной нагрузке значительно уменьшается, когда опора смещается внутрь на некоторое расстояние от положения обоих концов балки.

Например, балка и цилиндрический контейнер козлового крана, точка опоры которого немного смещается к середине, позволяют добиться эффекта снижения максимального изгибающего момента.

2. Разумное сечение балки

Чем больше коэффициент сечения при изгибе, тем меньше напряжение и выше несущая способность балки.

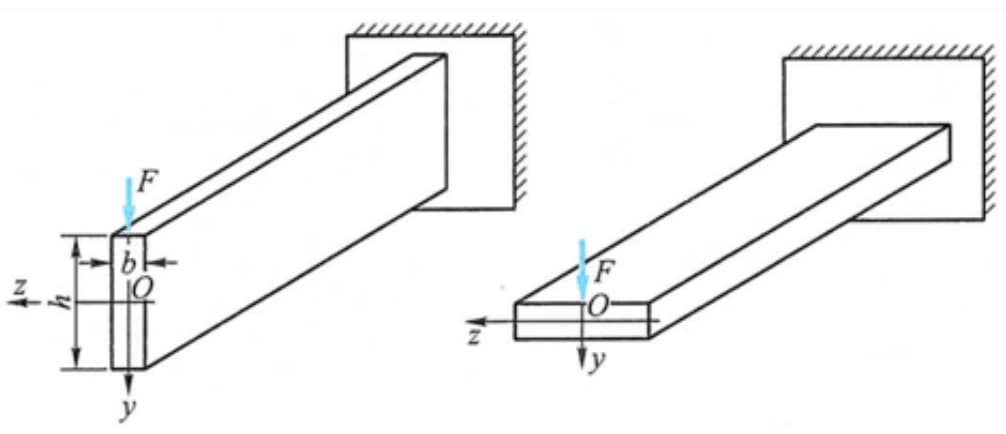
Например, когда балка нагружена в вертикальном направлении, коэффициент изгиба сечения больше, когда сечение расположено вертикально, поэтому целесообразнее располагать его вертикально, чем горизонтально.

Улучшая коэффициент изгиба секции, мы также надеемся использовать меньше материалов для достижения большей экономичности.

Поэтому отношение коэффициента изгиба сечения к площади сечения обычно используется для измерения рациональности конструкции сечения.

При одинаковой площади поперечного сечения прямоугольное сечение (высота больше ширины) целесообразнее круглого сечения, а I-образное или коробчатое сечение целесообразнее прямоугольного сечения.

Поэтому, чтобы полностью использовать материалы, их следует размещать как можно дальше от нейтральной оси.

При обсуждении разумной формы секции механические свойства материала также следует принимать во внимание.

Материалы с одинаковой прочностью на растяжение и сжатие (например, низкоуглеродистая сталь) должны иметь нейтральные осесимметричные сечения, такие как круглое, прямоугольное, I-образное, коробчатое и т. д.

Таким образом, максимальное растягивающее напряжение и максимальное сжимающее напряжение на верхнем и нижнем краях секции могут быть одинаковыми.

Для материалов с неодинаковой прочностью на растяжение и сжатие (таких как чугун, цемент и т.д.) следует принимать форму сечения с нейтральной осью, наклоненной в сторону растяжения.

Концепция равнопрочной балки

Все рассмотренные выше балки имеют одинаковое сечение, и коэффициент сечения при изгибе постоянен, но в общем случае изгибающий момент каждой секции балки меняется в зависимости от положения секции.

Расчет сечения равнополочной прямой балки должен выполняться с учетом максимального изгибающего момента, а максимальное напряжение в ней должно быть близко к допустимому.

Изгибающий момент на других участках мал, поэтому напряжение невелико, и материал используется не полностью.

Для экономии материалов и снижения собственного веса размер сечения может быть изменен таким образом, чтобы коэффициент изгиба сечения изменялся в зависимости от изгибающего момента.

Большее сечение используется там, где изгибающий момент больше, а меньшее - там, где изгибающий момент меньше.

Такая балка, сечение которой меняется вдоль оси, называется балкой переменного сечения.

Если максимальное нормальное напряжение в каждом сечении балки переменного сечения равно и равно допускаемому напряжению, она называется балкой равной прочности.