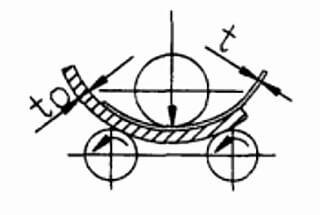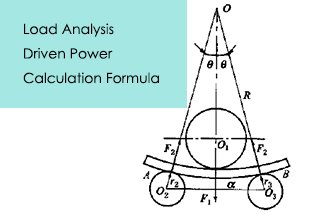
Вы когда-нибудь пытались рассчитать межосевое расстояние между роликами в станке? В этой статье блога мы рассмотрим простой метод определения этого важного измерения. Наш эксперт, инженер-механик, проведет вас через весь процесс, предоставив ценные сведения и практические примеры. К концу статьи вы будете иметь четкое представление о том, как решить эту распространенную проблему и улучшить свои навыки проектирования машин.
При изготовлении котлов и сосудов под давлением технология формовки является одним из основных производственных процессов.
В процессе формовки прокатка цилиндрического профиля является самым основным методом формовки. Прокатка требует больших трудозатрат. В основном процесс формовки осуществляется на симметричной трехвалковой гибочной машине. Однако из-за того, что толщина и диаметр цилиндрической части определяются в зависимости от условий производства, существует значительное количество спецификаций и разновидностей.
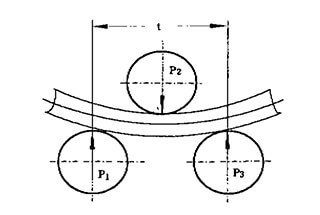
Точность кривизны после формовки зависит от параметра "H", который представляет собой межосевое расстояние между верхним и нижним роликами в конце прокатки.
Этот параметр обычно определяется по формуле (1).
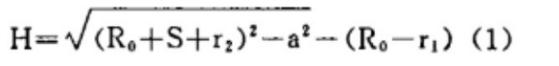
Может показаться, что в этой формуле нет ничего сложного, но для производителей совокупный объем работы оказывается значительным из-за различных спецификаций и разновидностей секций цилиндров.
Чтобы упростить и облегчить определение величины "H" при различных условиях, в данной статье будут использованы два следующих графических алгоритма.
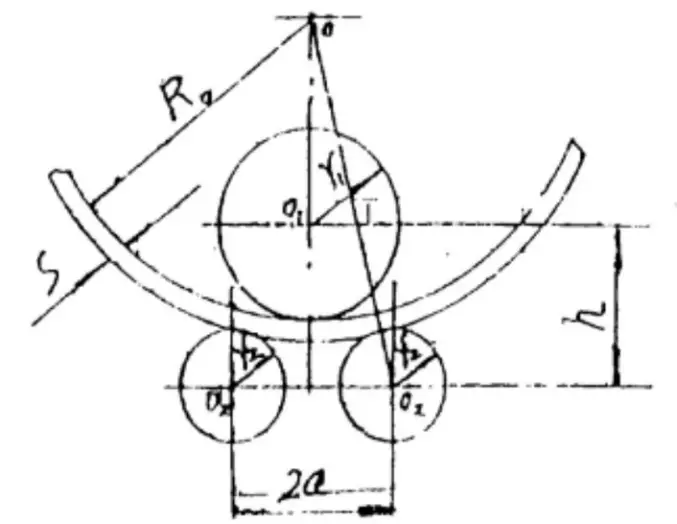
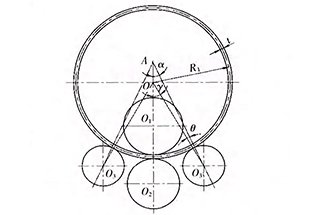
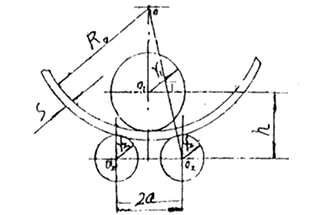
Рис. 1 Диаграмма конечного положения симметричного трехроликового вала листогибочный станок
Когда определенный тип листопрокатный станок заданы параметры a, r1 и р2 в приведенной выше формуле являются константами, только s и R0 являются переменными.
Поэтому, когда определенный тип листогибочный станок используется для раскатки любой толщины и радиуса кривизны, соответствующий основной параметр "h" может быть получен по следующему графовому алгоритму.
Сначала устанавливается прямоугольная система координат с ординатой a и абсциссой h.
Затем выполняется следующий чертеж в системе координат (показано на рис. 2)
Она должна пересечь OP = a на продольной оси, принять точку P за центр окружности и взять (R0 + S + r2) в качестве радиуса, чтобы положительная точка a находилась на поперечной оси пересечения дуг.
За центр окружности следует принять точку a, за R0 как радиус, и обратная точка B на поперечной оси дуги.
Затем точка B принимается за центр окружности, а R1 принимается за радиус пересечения дуги, а точка C находится в положительном направлении поперечной оси дуги.
Таким образом: OC = h.
Например,
Секции барабана с S = 20 мм и d = 2 000 мм прокатываются на симметричном трехвалковом листогибочном станке 70 × 4000.
Чтобы вычислить значение h.
Согласно полученным данным, R1 = 350 мм, R2 = 330 мм, 2a = 800 мм.
Согласно алгоритму графа (показан на рис. 2): h = 640 мм, который рассчитывается по формуле:
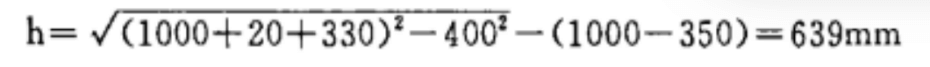
Абсолютная погрешность составляет всего 1 мм, что составляет 0,015% от истинного значения, что является достаточно точным показателем.
Если (R + S + r) превратить в подвижную линейку, это будет удобнее.
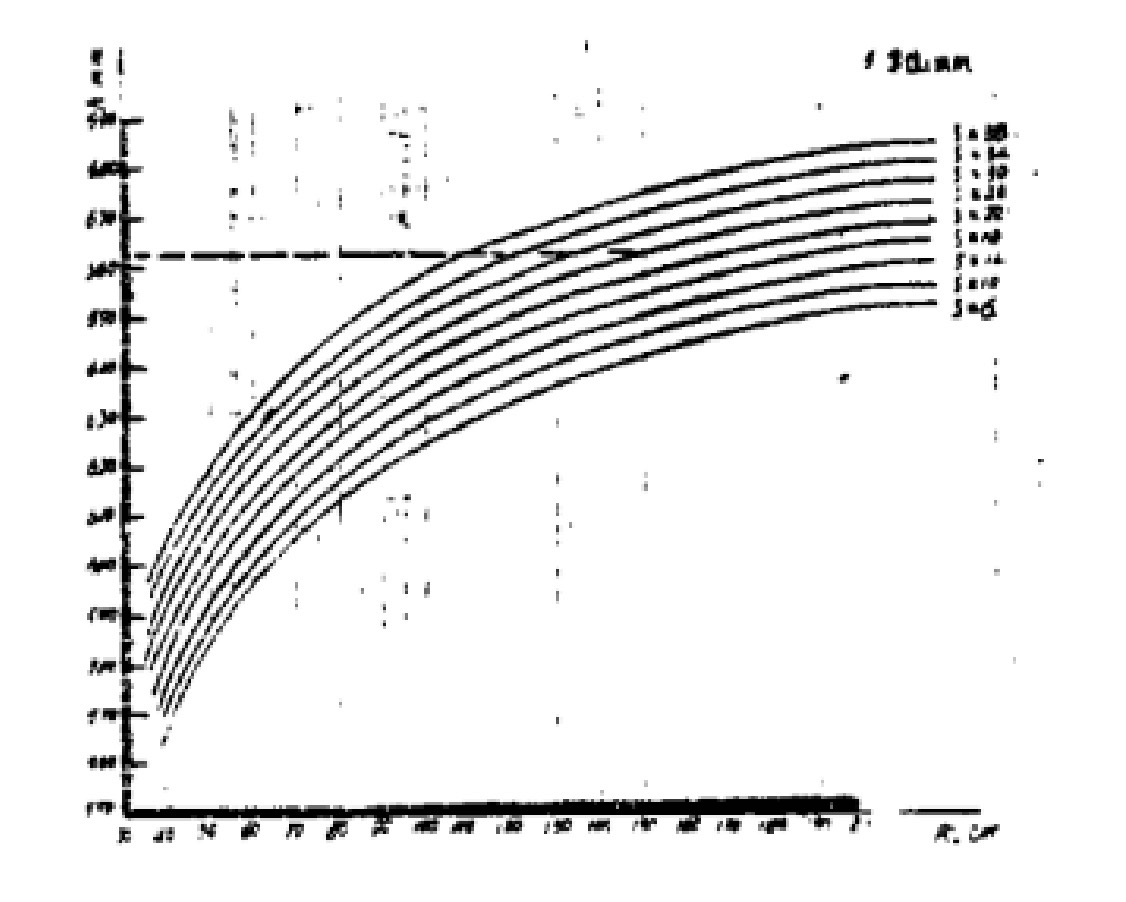
Рис. 2 Нормограмма для расчета "h"
Как известно, когда определенный тип изгиба Дана машина, ее параметры a, R1 и Р2 фиксированы.
Тогда, если кривая зависимости R0 и h при различной толщине пластины нарисовано в r0система координат -h, график общей точки R0 и h стального листа различной толщины на этом типе прокатная машина можно получить.
Очень удобно получать значение основного параметра "h" барабанной секции на листогибочных станках этого типа при самых разных условиях.
Ниже приведена диаграмма общих точек симметричной тройки 70 × 4000. роликовая пластина гибочный станок.
Известно: r1 = 350 мм, r2 = 330 мм, a = 400 мм
Итак:
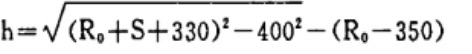
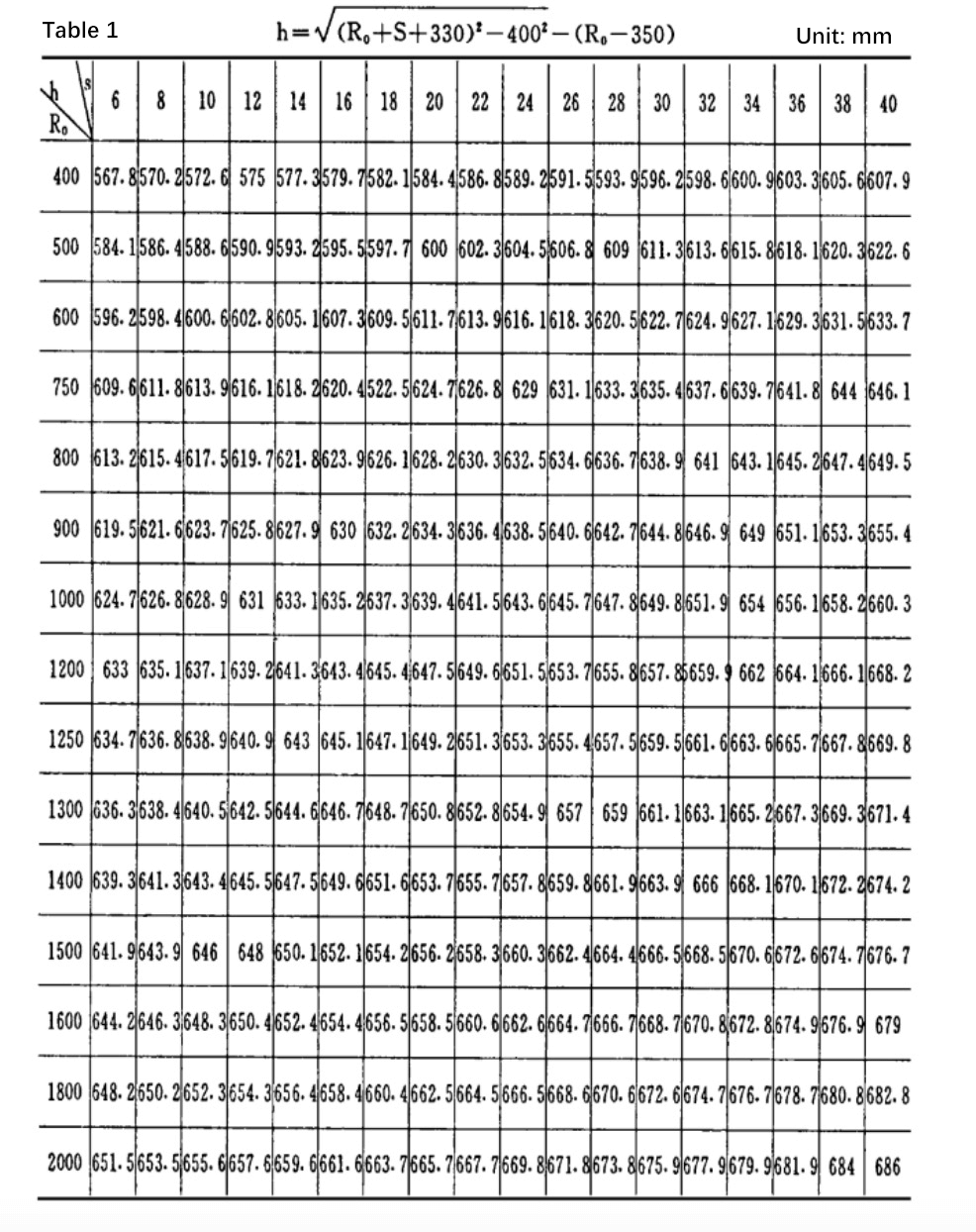
Таблица 1 представляет собой таблицу данных расчета и чертежа с интервалом s 2 мм.
Согласно практическому опыту, толщина прокатная машина обычно составляет 6 ≤ s ≤ 40 (мм).
Как правило, радиус секции прокатного барабана составляет 400 ≤ R0 ≤ 200 (мм).
Поэтому этот диапазон используется в качестве расчетного диапазона чертежей.
Из таблицы 1 видно, что значение "n" в основном эквивалентно толщине листа s, когда определенный тип листогибочной машины используется для прокатки определенного количества R0.
Погрешность между фактическим и действительным значением составляет менее 0,05%.
Однако при изгибе медной пластины происходит как пластическая, так и упругая деформация.
Поэтому после разгрузки происходит определенное восстановление упругости.
Поэтому в реальном производстве стоимость должна быть немного меньше фактической.
Таким образом, если использовать закон эквивалентного изменения двух, рисунок упростится, а упругие springback после фактического изгиба можно компенсировать.
В то же время линия графика может быть уменьшена, а значение "h", соответствующее любому S, может быть определено при определенном R0.
Первый графовый алгоритм является универсальным, а второй - для определенного типа листогибочного станка, которому соответствует специальное (k-R0-S) копунктный граф.
Результаты использования двух графовых алгоритмов в обучении очень хороши и значительно просвещают студентов.
В частности, последний метод обладает определенной практичностью.
Предлагается, чтобы производитель листогибочного станка настроил общую принципиальную схему (n-R0-S) на прокатная машина или в руководстве, что принесет большое удобство для реального производства производителя.