Как простая система кулачков и последователей может привести к эффективному и точному движению в сложных механизмах? В этой статье рассматриваются тонкости проектирования кулачковых приводных механизмов, объясняются различные типы кулачков и последователей, пути их движения и способы достижения оптимальной производительности. Начиная с основных компонентов и заканчивая передовыми методами проектирования, читатели получат ценные сведения о создании высокоэффективных кулачковых систем. Ожидайте получить практические советы и подробный анализ, которые улучшат ваше понимание и применение кулачковых механизмов в инженерных проектах.
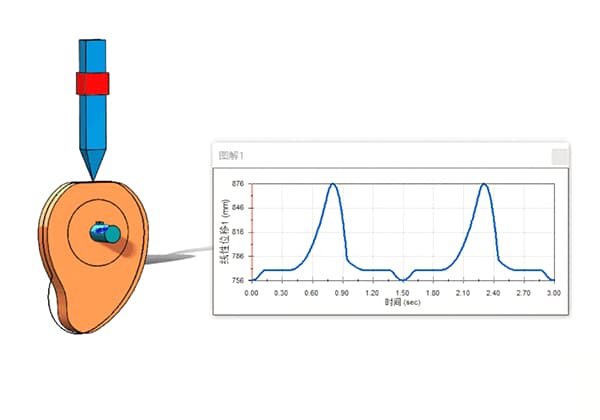
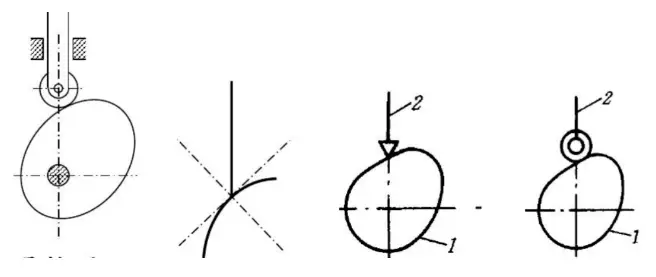
Кулачковый механизм обычно состоит из двух подвижных частей - кулачка и последователя, которые крепятся к раме. Кулачковое устройство очень универсально и может генерировать практически любое произвольное движение.
Кулачок можно определить как деталь с изогнутой поверхностью или канавкой. Качаясь или вращаясь, другой компонент, последователя, может обеспечить заданное движение. Для получения возвратно-поступательного движения путь следящего элемента в основном ограничен пазом.
Некоторые механизмы, полагаясь на собственный вес во время обратного хода, используют пружины в качестве возвращающей силы для достижения точных движений. Другие используют направляющие рельсы для перемещения по определенным траекториям.
По форме кулачки можно разделить на три типа: дисковые, подвижные и цилиндрические.
В соответствии с концами последователи можно разделить на три типа: остроконечные, роликовые и плоскодонные.
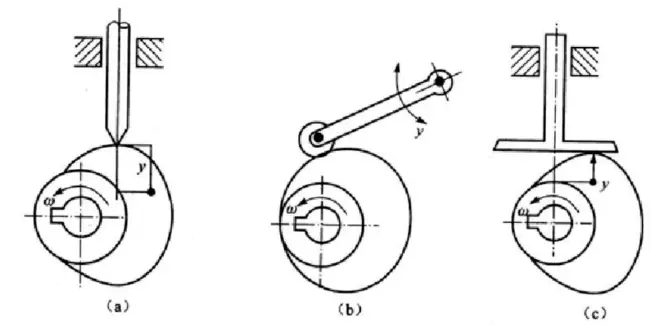
Из-за точечного контакта остроносого следящего элемента с кулачком, который приводит к высоким напряжениям и быстрому износу, он не подходит для низкоскоростных кулачковых механизмов с большими ударами. Роликовый привод позволяет устранить эти недостатки.
Чтобы повысить эффективность передачи, мы также можем ввести последователя с плоским дном, которое перпендикулярно направлению силы на нижней поверхности.
Компоненты трансмиссии, которые мы рассматривали ранее, имеют форму прямолинейного движения, но они также могут быть в форме колебательного движения. Первый вариант называется прямолинейным, а второй - качающимся.
Мы также можем сделать так, чтобы центр вращения кулачка не совпадал с линейной траекторией движения последователя. В этом случае мы называем его смещенным. Соответственно, если центр вращения находится на линейной траектории движения последователя, мы можем назвать его концентрическим.
Кроме того, мы можем рассмотреть методы поддержания высоконапряженных связей блокировки и разделить механизм на геометрическую блокировку и силовую блокировку.
Комбинируя форму кулачка, конец следящего элемента и характер движения следящего элемента, мы можем определить название разработанного механизма, например: дисковый кулачок с остроносым следящим элементом прямого действия (относительное положение следящего элемента + конец следящего элемента + характер движения следящего элемента + форма кулачка).
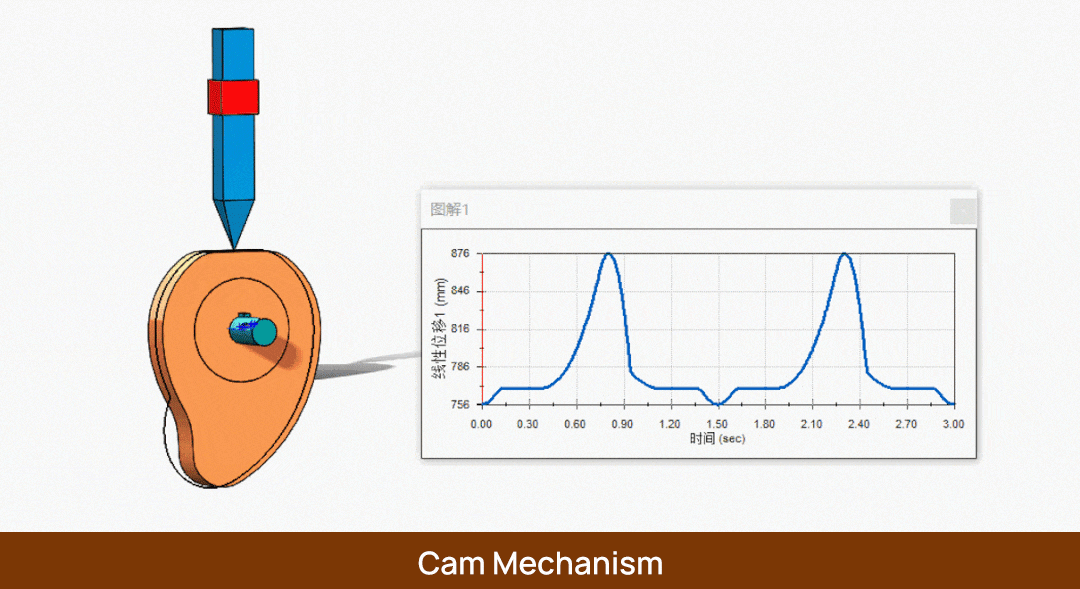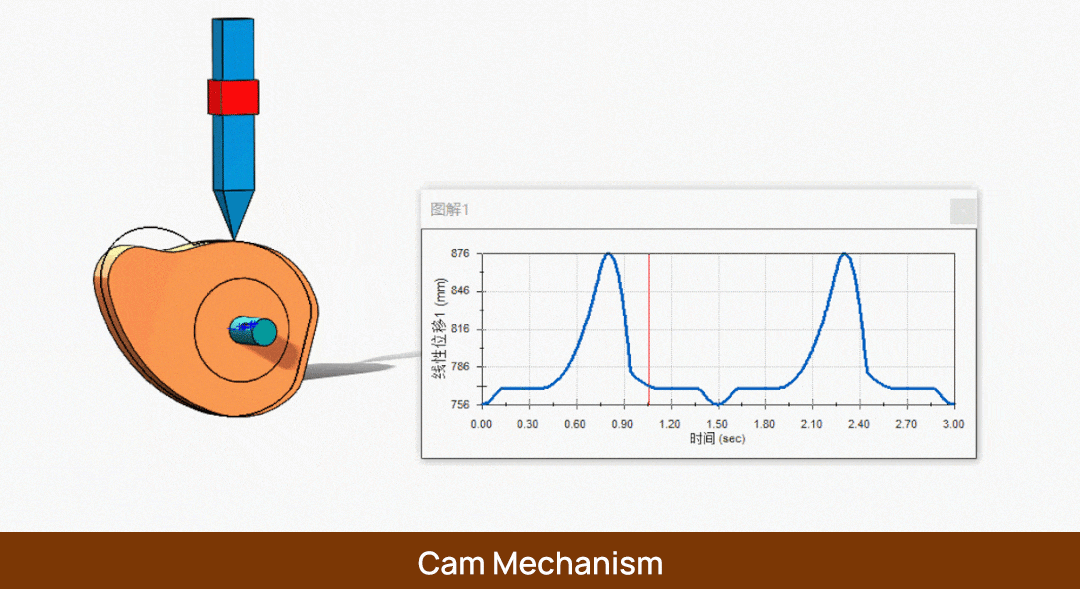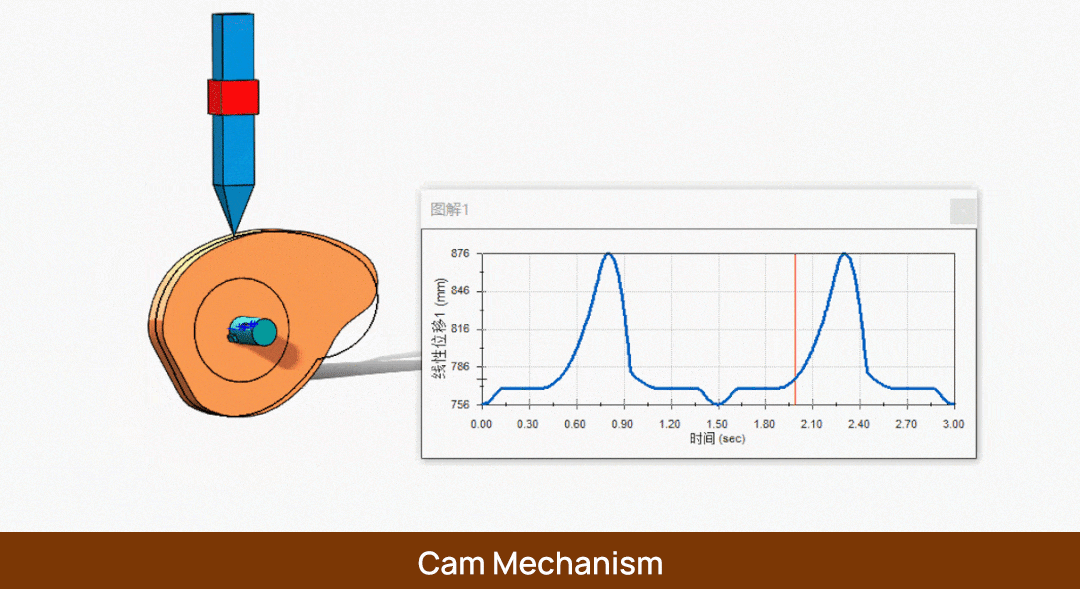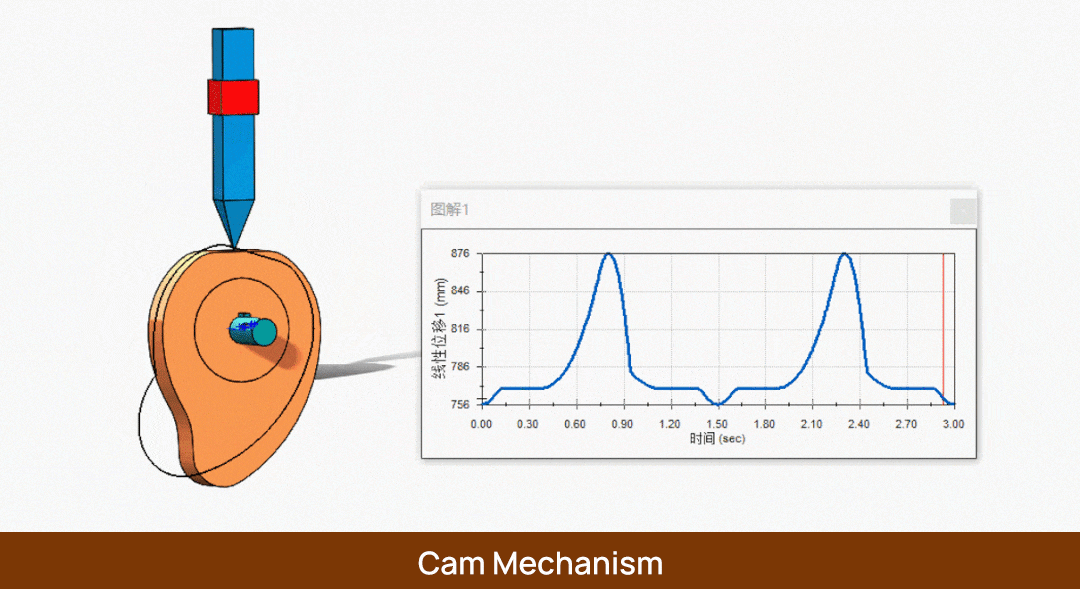
Во-первых, у нас есть кулачок с установленным на нем последователем. Когда кулачок поворачивается с угловой скоростью ω на φs градусов, следящий элемент не перемещается. В этот момент мы называем угол φs углом остановки, а соответствующую ему окружность - базовой окружностью. Аналогично, радиус этой окружности называется радиусом базовой окружности r0.
Затем, когда мы продолжаем вращать кулачок с угловой скоростью ω на φ градусов, следящий элемент поднимается на h. В этот момент мы называем φ углом хода, а h - ходом.
Затем, когда следящий элемент достигает точки h, мы оставляем его на некоторое время. Тем временем кулачок поворачивается на угол φs', который соответствует углу подъема.
Наконец, нам нужно вернуть следящий элемент в исходное положение, поэтому мы поворачиваем кулачок на φ'. В это время последователь возвращается в исходную точку. Угол φ' мы называем углом возврата.
Существует два основных метода проектирования кулачковых механизмов: графический и аналитический.
Первый вариант относительно прост: требуется только предоставить требуемую диаграмму толчкового движения, а затем получить соответствующую контурную кривую на основе зависимости угла от процесса, представленной на диаграмме.
Точность не очень высокая. Последний вариант является расчетным, и его расчет относительно сложен, что подходит для проектирования кулачковых механизмов с высокими требованиями к точности.
Как основатель MachineMFG, я посвятил более десяти лет своей карьеры металлообрабатывающей промышленности. Мой обширный опыт позволил мне стать экспертом в области производства листового металла, механической обработки, машиностроения и станков для обработки металлов. Я постоянно думаю, читаю и пишу об этих предметах, постоянно стремясь оставаться на переднем крае своей области. Позвольте моим знаниям и опыту стать преимуществом для вашего бизнеса.
RU 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT 
PT_BR 
KO 
TR