Вы когда-нибудь задумывались о том, как мельчайшие измерения могут повлиять на качество работы оборудования? Эта статья погружает в увлекательный мир механических измерений, показывая, как точность размеров, углов и форм обеспечивает высочайшее качество продукции и повышает эффективность производства. Приготовьтесь узнать, какую решающую роль играют измерительные технологии в современном производстве и как они могут повысить конкурентоспособность отрасли.

Развитие машиностроения отражается в модернизации измерительной техники, возможности реализации принципа взаимозаменяемости производства и других аспектах, связанных с геометрическими характеристиками механических деталей, допусковыми посадками и механическими измерениями.
Они напрямую отражают качество продукции и конкурентоспособность предприятий.

Механические измерения играют важную роль в машиностроении и являются решающим фактором в обеспечении качества продукции и эффективности производства. Важность измерительной техники может быть отражена несколькими способами, в том числе:
Контролируйте производственный процесс:
Измерительная техника обеспечивает метод управления механическим производством, делая его более точным и повышая качество.
Улучшение качества продукции:
Измерительная техника точно определяет пригодность материалов и технологии производства, повышая тем самым качество продукции.
Повышение конкурентоспособности:
Передовые измерительные технологии позволяют повысить эффективность производства, снизить затраты и повысить конкурентоспособность предприятий.
Реализуйте интеллектуальное производство:
С непрерывным развитием науки и техники диапазон измерений расширился: можно измерять от нанометров до нескольких сотен метров.
Улучшите уровень процесса:
Измерительная техника позволяет проверить, соответствуют ли обрабатываемые детали проектным размерам, соответствует ли точность сборки заданному значению, а также обеспечить стабильность и надежность производственного процесса.

На производстве, чтобы обеспечить качество продукции, гарантировать взаимозаменяемость компонентов, проанализировать технологию обработки деталей и принять профилактические меры по предотвращению образования отходов, необходимо измерять и проверять размеры, углы, геометрические формы, взаимное расположение геометрических элементов, шероховатость поверхности, и другие технические условия заготовок и компонентов.
Измерение относится к сравнению измеряемого объекта со стандартной единицей измерения, определяя таким образом экспериментальный процесс измеряемого объекта.
Инспекция необходимо только определить, соответствует ли деталь требованиям, без измерения конкретных числовых значений. Инспекция - это общий термин для измерения и проверки.
Геометрические измерения В основном относится к измерению параметров геометрических размеров и форм поверхностей различных механических компонентов.
К геометрическим параметрам относятся размеры длины, угловые параметры, координатные (позиционные) размеры, параметры геометрической формы и положения поверхности, шероховатость поверхности и т.д. Геометрические измерения являются важной мерой для обеспечения качества механических изделий и достижения взаимозаменяемости продукции.

Геометрические объекты измерения разнообразны, и разные объекты измерения имеют разные измеряемые величины.
Например, измеряемые величины отверстий и валов в основном представляют собой диаметры; измеряемые величины коробчатых деталей включают длину, ширину, высоту, расстояние между отверстиями и т.д.; сложные детали имеют сложные измеряемые величины, такие как погрешности спирали винтов и фрезы для прокатки.
Однако, независимо от формы, измеряемые параметры можно разделить на два типа: длина и угол, а сложные величины можно рассматривать как комбинации длины и угла.
Полный процесс измерения должен включать следующие четыре элемента:
(1) Измеряемый объект
С точки зрения характеристик геометрических величин, объекты измерения можно разделить на длину, угол, погрешность формы, шероховатость поверхности и т.д.
По характеристикам измеряемых деталей их можно разделить на квадратные, валовые, конические, коробчатые, кулачковые, ключевые, резьбовые, зубчатые и различные инструменты.
(2) Единица измерения
Единицы длины включают метры (m), миллиметры (mm) и микрометры (μm), а единицы угла - градусы (°), минуты (′), секунды (″), радианы (rad) и микрорадианы (μrad).
(3) Метод измерения
Означает сумму методов, измерительные инструменты или приборы, и условия измерения, используемые для выполнения задачи измерения.
Основные методы измерения включают в себя прямое и косвенное измерение, абсолютное и относительное измерение, контактное и бесконтактное измерение, одностороннее и комплексное измерение, ручное и автоматическое измерение, измерение процесса и окончательное измерение, активное и пассивное измерение и т.д.
Соответствующий метод измерения должен быть выбран наиболее экономичным, исходя из требований к измеряемому объекту.
(4) Точность измерения
Точность измерения - это степень соответствия между результатом измерения и истинным значением измеряемого объекта.
Не чем выше точность, тем лучше, а следует выбрать наиболее экономичный способ, исходя из требований к точности измеряемого объекта.
В Китае приняты юридические единицы измерения, основанные на Международной системе единиц.
1. Единицы длины
В машиностроении обычно используются миллиметры (мм) и микроны (мкм). Миллиметры - наиболее часто используемые единицы измерения в механических измерениях.
При использовании миллиметров на механических чертежах необходимо указывать только размерные цифры, а единицы измерения можно не указывать.
Основными единицами измерения длины в английском языке являются футы (ft) и дюймы (in).
2. Единицы измерения плоского угла
В юридических измерениях основной единицей измерения плоского угла является радиан (рад). Радиан - это плоский угол между двумя радиусами окружности, которые отсекают на окружности дугу, равную по длине радиусу.
В машиностроении в качестве единиц измерения угла наклона плоскости обычно используются градусы (°).
1° = π/180 (рад)
| Название и символ устройства | Преобразование единиц измерения | Название и символ устройства | Преобразование единиц измерения |
| Длина m миля миля ft в йд mil - A | 1852m 1609.344m 0.3048m 0.0254m 0.9144m 25.4×10-6m 10-10m 10-15m | (‘) (“) Время s мин h d | (π/10800)рад (π/648000)рад 60s 3600s 86400s |
| Область m2 ха a миля2 ft2 в2 | 10000m2 100m2 2.58999×106m2 0.0929030m2 6.4516×10-4m2 | Скорость м/с км/ч м/мин миля/ч фут/с в/с | 0,514444 м/с 0,277778 м/с 0,0166667 м/с 0,44704 м/с 0,3048 м/с 0,0254 м/с |
| Объем/емкость m3 L,(l) ft3 в3 UKgal USgal | 10-3m3 0.0283168 m3 1.63871×10-5 m3 4.54609 дм3 3.78541 m3 | Ускорение м/с2 фут/с2 Гал Угловая скорость рад/с об/мин (°)/мин (°)/s | 10-2м/с2 (π/30) рад/с 0,0002 рад/с 0,01745 рад/с |
Классификация на основе того, является ли измеряемый параметр непосредственно измеряемым или нет.
(1) Прямое измерение
Измеряемая величина может быть непосредственно считана со считывающего устройства измерительного прибора.
Например, измерение диаметра окружности методом высоты хорды, измерение диаметра вала или отверстия с помощью штангенциркуля или микрометра, а также измерение угла с помощью транспортира.
(2) Косвенное измерение
Измеряемая величина получается косвенно (например, путем вычисления) на основе измеряемой величины, которая имеет с ней определенную связь.
Например, измерение диаметра круга путем измерения длины хорды S и высоты хорды H, чтобы вычислить диаметр круга D.
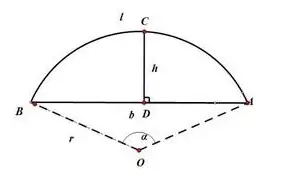
Для уменьшения погрешностей измерений обычно используются прямые измерения. Косвенные измерения могут использоваться, когда измеряемую величину нелегко измерить напрямую.
2. Классификация на основе того, представляет ли отображаемое значение все измеренное количество
(1) Абсолютное измерение
Фактическое значение измеряемой величины может быть непосредственно считано с измерительного прибора.
При использовании абсолютного метода измерения диапазон измерения средства измерения должен превышать размер измеряемой величины.
(2) Относительное измерение (сравнительное измерение)
Можно непосредственно получить только отклонение измеряемой величины от стандартной. Диапазон измерений очень узкий.
Например, использование блока калибров в качестве эталона, измерение размеров длины на оптической измерительной машине.
Как правило, точность относительных измерений выше, чем абсолютных.
3. Классификация по наличию контакта измерительной головки с измеряемой поверхностью во время измерения
(1) Измерение контакта
Во время измерения измерительная головка измерительного прибора непосредственно соприкасается с измеряемой поверхностью, при этом возникает механическое измерительное усилие, как, например, при измерении размеров микрометром.
(2) Бесконтактное измерение
Во время измерения измерительная головка прибора не контактирует непосредственно с измеряемой поверхностью, а контактирует с деталью через другие среды (такие как свет, воздух и т.д.), например, при измерении шероховатости поверхности оптическим профилометром.
Контактное измерение может вызвать упругую деформацию соответствующих частей измеряемой поверхности и измерительного прибора, что влияет на точность измерения, в то время как бесконтактное измерение не имеет такого эффекта.
4. Классификация на основе количества параметров, измеряемых в одном измерении
(1) Измерение одного предмета
Каждый параметр измеряемой детали измеряется отдельно.
(2) Комплексная оценка
Он измеряет комплексный показатель, отражающий связанные параметры детали.
Комплексное измерение, как правило, имеет более высокую эффективность и более надежно обеспечивает взаимозаменяемость деталей.
Часто используется для контроля готовых деталей. Измерение отдельных элементов позволяет определить погрешности каждого параметра в отдельности и обычно используется для анализа процесса, контроля процесса и для измерения заданных параметров.
Ошибка обработки
В процессе производства обработанных деталей трудно достичь идеального состояния размеров, формы, микрогеометрии (шероховатости поверхности) и взаимного расположения деталей из-за влияния различных факторов, таких как ограничение точности станка, погрешности угла заточки инструмента, недостаточная жесткость технологической системы.
Любой метод обработки не может обеспечить абсолютную точность деталей. Даже партия обработанных деталей может иметь различия, обусловленные различными факторами.
Даже при одинаковых условиях обработки размеры одной и той же партии заготовок могут быть разными.
Для выполнения определенных требований к точности необходимо контролировать погрешности в определенном диапазоне. Для того чтобы удовлетворить требованиям взаимозаменяемости и сделать геометрические параметры деталей с одинаковыми характеристиками близкими друг к другу, необходимо также контролировать погрешности обработки.
Проявление ошибок обработки обычно имеет несколько форм:
(1) Погрешность размеров: Погрешность в размере поверхности самой детали (например, погрешность диаметра цилиндрической поверхности) и погрешность в размере поверхности между деталями (например, расстояние между отверстиями).
(2) Ошибка формы: Степень отклонения фактической поверхности детали от идеальной по форме, например, погрешность цилиндричности цилиндрической поверхности, погрешность плоскостности плоскости и т.д.
(3) Ошибка позиционирования: Степень отклонения фактического положения поверхности, оси или плоскости симметрии от идеального положения, например, ошибка параллельности и перпендикулярность погрешность между двумя поверхностями.
(4) Качество поверхности: Микроскопическая шероховатость с небольшими интервалами и крошечными пиками и долинами, остающаяся на поверхности заготовки после обработки.
При этом одновременно присутствуют несколько типов погрешностей, среди которых размерная погрешность является самой основной. Под точностью детали понимается степень соответствия между фактическими и идеальными значениями геометрических параметров.
Чем меньше разница между фактическими и идеальными значениями геометрических параметров, то есть чем меньше погрешность, тем выше точность обработки.
Поэтому точность детали выражается величиной погрешности. Видно, что понятия "точность" и "погрешность" - это лишь разные фокусы при оценке геометрических параметров детали, но по сути одно и то же.
Ошибка измерения
Разность между действительным значением измеряемой величины и истинным значением измеряемой геометрической величины называется погрешностью измерения. Погрешность измерения выражается в абсолютной погрешности или относительной погрешности.
Абсолютная погрешность: Абсолютная погрешность δ - это разность между действительным значением измеряемой величины и истинным значением, которая составляет:

где X - фактическое измеренное значение (измеряемая величина), а X0 - истинное или согласованное истинное значение.
Относительная погрешность:
Относительная погрешность - это отношение абсолютного значения абсолютной погрешности к истинному значению измеренной геометрической величины. Поскольку истинное значение измеряемой геометрической величины получить невозможно, для оценки вместо истинного значения часто используют измеренное значение измеряемой геометрической величины, т.е:

Существует несколько факторов, способствующих ошибке измерения, в том числе:
1. Погрешность измерительных инструментов:
Погрешность измерительных инструментов - это погрешность, присущая самому измерительному инструменту, включая погрешности при проектировании, изготовлении и использовании измерительного инструмента.
2. Ошибка метода:
Погрешность метода - это погрешность, вызванная несовершенством метода измерения (включая неточные расчетные формулы, неправильный выбор метода измерения, неточную установку и позиционирование заготовки и т.д.), которая может привести к ошибкам измерения.
Например, при контактном измерении измерительная сила измерительной головки может вызвать деформацию измеряемой детали и измерительного устройства, что приведет к ошибкам измерения.
3. Экологическая ошибка:
Погрешность окружающей среды означает погрешность, вызванную тем, что окружающая среда не соответствует стандартным условиям измерения во время измерения, что может привести к ошибкам измерения.
Например, температура, влажность, атмосферное давление, освещение (вызывающее параллакс), вибрация, электромагнитные поля и т.д., не соответствующие стандартам, могут стать причиной ошибок измерений, среди которых влияние температуры особенно заметно.
Например, при измерении длины стандартная температура окружающей среды составляет 20℃, но при реальном измерении температура измеряемой детали и измерительного инструмента будет отличаться от стандартной температуры, а коэффициент линейного расширения материала измеряемой детали и измерительного инструмента будет разным, что приведет к некоторым ошибкам измерения.
Поэтому температуру окружающей среды следует разумно контролировать в соответствии с требованиями к точности измерений, чтобы уменьшить влияние температуры на точность измерений.
4. Человеческая ошибка:
Под человеческой ошибкой понимаются ошибки, вызванные человеческим фактором, которые могут привести к ошибкам измерений.
Например, неправильное использование измерительных приборов, неточное выравнивание измерений, ошибки в считывании или оценке, допущенные лицом, производящим измерения, и т. д. - все это может привести к ошибкам измерений.

Классификация ошибок измерения:
1. Систематическая ошибка:
(1) Постоянная систематическая ошибка:
Постоянная систематическая погрешность - это погрешность измерения, абсолютное значение и знак которой остаются неизменными при многократном измерении одной и той же величины в определенных условиях измерения.
Например, погрешность стандартного блока, используемого для настройки прибора, оказывает одинаковое влияние на результаты каждого измерения. Этот тип погрешности можно исключить из результатов измерений с помощью метода коррекции.
(2) Переменная систематическая ошибка:
Абсолютное значение и знак погрешности в процессе измерения изменяются по определенному правилу.
Например, погрешность индикации, вызванная эксцентричной установкой циферблата индикатора, представляет собой периодическое изменение по синусоидальному закону, и эта погрешность измерения может быть устранена методом компенсации.
2. Случайная ошибка:
Случайная погрешность - это погрешность измерения, которая изменяется случайным образом, с непредсказуемыми изменениями абсолютного значения и знака при многократном измерении одной и той же величины в определенных условиях измерения.
Случайная погрешность в основном вызвана случайными или неопределенными факторами в процессе измерения и обусловлена многими временными и неконтролируемыми факторами.
Однако при повторных измерениях погрешности подчиняются статистическим законам.
Поэтому для их решения часто используются теория вероятностей и статистические принципы.
При практических измерениях, чтобы уменьшить случайные ошибки, одно и то же количество может быть измерено несколько раз, а в качестве результата измерения может быть взято среднее арифметическое значение.
3. Грубая ошибка:
Под грубой погрешностью понимается погрешность измерения, которая превышает ожидаемую погрешность измерения при определенных условиях измерения, что приводит к значительному искажению результата измерения. Измеренное значение, содержащее грубые ошибки, называется выбросом.
Причины грубых ошибок могут быть субъективными или объективными. К субъективным причинам относятся ошибки считывания, вызванные небрежностью измерителя, а к объективным - ошибки измерения, вызванные внезапными внешними вибрациями.
Поскольку грубые ошибки существенно искажают результаты измерений, их следует устранять в соответствии с критериями выявления грубых ошибок при обработке данных измерений.
Следует отметить, что разделение на систематические и случайные ошибки не является абсолютным, и при определенных условиях они могут трансформироваться друг в друга.
При измерениях необходимо проводить серьезные, тщательные и скрупулезные наблюдения и удалять грубые ошибки из серии данных измерений. При анализе погрешностей в основном анализируются систематические и случайные погрешности.
Хотя случайные ошибки нельзя исправить или устранить, их размер и характер можно оценить с помощью теории вероятности и статистических методов, и необходимо приложить усилия, чтобы уменьшить их влияние.
Грубые ошибки имеют относительно большое значение, и их следует по возможности избегать при измерениях.
Если грубые ошибки уже произошли, их следует устранить в соответствии с критериями выявления грубых ошибок. Обычно используется критерий "3σ", также известный как правило трех сигм.

Чтобы обеспечить взаимозаменяемость деталей, используются допуски для контроля погрешностей.
Допуски должны быть рассчитаны в соответствии со стандартными нормами, а ошибки, неизбежно возникающие при обработке, должны контролироваться, чтобы готовые детали находились в пределах заданного диапазона допусков для взаимозаменяемости.
Исходя из предпосылки удовлетворения функциональных требований, значение допуска должно быть установлено как можно больше, чтобы получить наилучший экономический эффект.
Таким образом, ошибки возникают в процессе производства, в то время как допуски определяются конструкторами. Если погрешность детали попадает в диапазон допусков, то это квалифицированная деталь. Однако если погрешность выходит за пределы допуска, то это несоответствующая деталь.
Выбор количества цифр в измеряемом результате - распространенная проблема, возникающая в процессе измерения.
Количество значащих цифр в результатах измерений не должно быть слишком большим, что может привести к ошибочному мнению о высокой точности измерений.
В то же время оно не должно быть слишком малым, что может привести к потере точности. Поэтому количество значащих цифр результата измерения должно быть определено правильно, исходя из величины погрешности измерения.
Например, при измерении длины объекта стальной линейкой со значением деления 1 мм, длина составляет 123,4 мм, где 123 мм - это непосредственно показания стальной линейки, и они точны.
Последняя цифра, 0,4 мм, оценивается человеческим глазом и является ненадежной или сомнительной. Измеренные данные должны быть выражены таким образом: последняя цифра - это сомнительная цифра, а ошибка приходится на эту цифру.
Когда количество значащих цифр определено, принцип определения последней значащей цифры следующий:
(1) Если первая значащая цифра после последней значащей цифры больше 5, то прибавьте 1 к последней значащей цифре, а если она меньше 5, то не учитывайте ее.
(2) Если первая цифра после последней значащей цифры равна 5, последнюю значащую цифру следует привести к четному числу (добавить 1, если последняя значащая цифра нечетная, и оставить прежней, если она четная).
Например, если значащие цифры зарезервированы до третьего десятичного знака, то значащие цифры выглядят следующим образом:
3.14159 - значимые цифры 3.142
(3) При операциях сложения и вычитания количество десятичных знаков, которые необходимо зарезервировать, должно быть наименьшим среди всех чисел, например:
60.43 + 12.317 + 5.022 - 77.769 ≈ 77.77
(4) В операциях умножения и деления число значащих цифр должно быть наименьшим, например:
2352 × 0.211 = 496.272 ≈ 496
0.0222 × 34.5 × 2.01= 1.539459 ≈ 1.54.
(5) Количество цифр в логарифмических операциях должно быть равно количеству эффективных цифр в действительном числе.
(6) При операциях экспоненцирования количество значащих цифр в экспоненте должно быть таким же, как и количество значащих цифр в основании.
(7) В операциях с квадратным корнем количество значащих цифр должно быть таким же, как количество значащих цифр в радиканде.
(8) Если в операции участвуют математические константы, такие как π и 2, определите их значащие цифры в соответствии с описанным выше методом. Для обеспечения точности конечного результата операции эти константы могут быть соответствующим образом выбраны на 1-2 разряда.
(9) Для значений, представляющих точность измерений, таких как предельные погрешности измерений и стандартные отклонения, следует брать только одну или две значащие цифры, а последняя цифра должна соответствовать последней цифре соответствующего результата измерения.
Например,
34,0234 ± 0,00021 следует записать как 34,0234 ± 0,0002.
Измерение длины - важнейший аспект механических измерительных систем. Существует несколько методов измерения длины, в том числе:
Сила и крутящий момент - важнейшие параметры механических систем. Некоторые распространенные методы их измерения:
Измерение давления необходимо для решения задач механики жидкостей. Стандартными методами измерения давления являются:
Температура - это фундаментальный параметр механических систем, влияющий на свойства материала и производительности. К распространенным методам измерения температуры относятся:
Измерение расхода необходимо для решения задач гидромеханики, например, в трубопроводных системах или при управлении технологическими процессами. Некоторые методы измерения расхода включают в себя:
Эти методы представляют собой подборку распространенных методик, используемых для механических измерений, и служат основой для понимания сложности и важности точных измерений в современных инженерных приложениях.
К числу важнейших инструментов для инженерных измерений относятся измерительные ленты, верньерные штангенциркули, микрометры, циферблатные манометры, инженерные квадраты, транспортиры и термопары. Все эти инструменты вместе обеспечивают надежный способ точного измерения различных механических величин.
Измерения играют ключевую роль в инженерном деле, поскольку позволяют инженерам:
Международная система единиц (СИ) - это наиболее распространенная система измерения механических величин. Некоторые стандартные единицы включают:
В машиностроении обычно используются различные типы измерений, такие как линейные, угловые и температурные. Другие важные виды измерений включают силу, давление, поток жидкости и вибрацию. Эти измерения необходимы для проектирования, производства и обслуживания механических систем и компонентов.


