Собственная частота и резонансная частота: Разница объяснена

В повседневном анализе мы часто путаем собственную частоту и резонансную частоту и думаем, что это одно и то же.

На самом деле, это не так уж и строго.

Собственная частота - это показатель собственных характеристик конструкции, а резонансная частота - показатель отклика конструкции на внешние воздействия.

Свободные колебания пружинной системы с одной степенью свободы

Система с одной степенью свободы - это система, в которой положение может быть полностью определено только одной обобщенной координатой в любой момент времени. Проще говоря, сила, действующая на тело, направлена только в одну сторону. Движение куклы на рисунке ниже можно представить как систему пружина-масса.

Упрощенная модель системы пружинных масс показана на следующем рисунке.

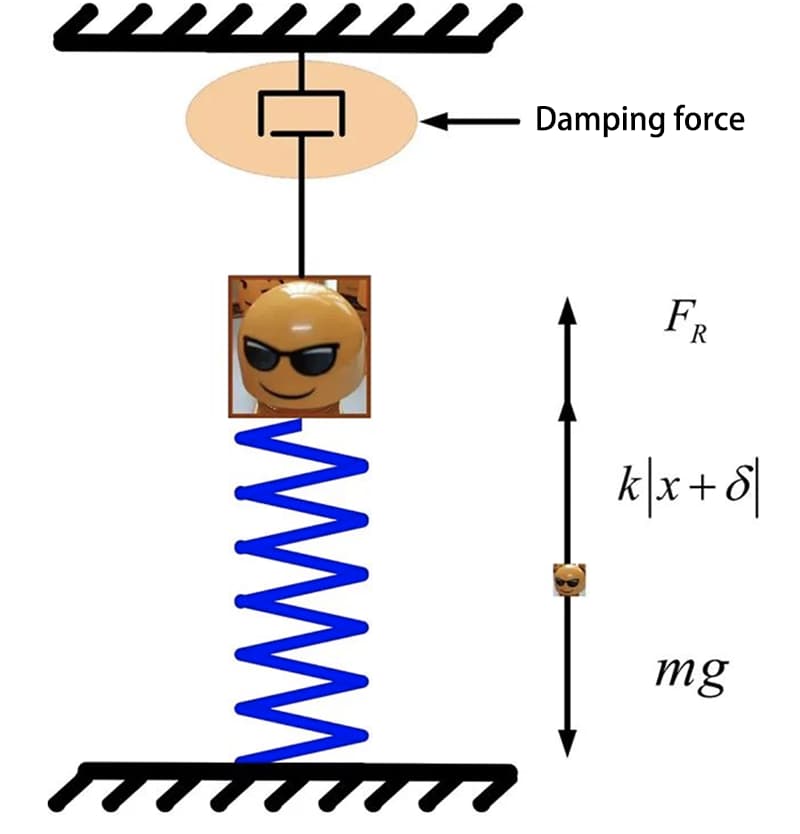
За начало координат принимается положение статического равновесия блока пикапа, которое считается положительным, если он движется вертикально вниз вдоль направления деформации пружины. Расстояние между блоком и положением равновесия можно представить как x, а дифференциальное уравнение движения блока можно выразить как:

Где, m - масса блока, k - жесткость пружины, c - коэффициент вязкости, 2n=c/m - коэффициент демпфирования, а когда коэффициент демпфирования равен нулю, то это соответствует недемпфированной колебательной системе.

Собственная частота Pn:

Собственная частота зависит только от массы и жесткости и не зависит от таких факторов, как демпфирование. Структурные граничные соединения, свойства материалаФорма и другие факторы могут влиять на собственную частоту, но это влияние отражается на жесткости и массе и не является окончательным определяющим фактором.

Вынужденные колебания пружинной системы при гармоническом возбуждении

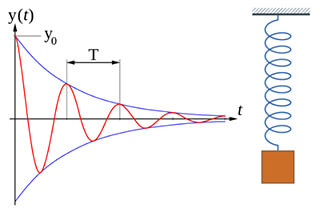
Свободные колебания - это колебания системы без внешнего возбуждения, а траектория движения связана с начальным состоянием и естественными характеристиками.

Вынужденная вибрация - это вибрация, возникающая в системе под действием внешнего возбуждения.

Внешнее возбуждение обычно представляет собой периодическую или апериодическую функцию времени, среди которых простейшее гармоническое возбуждение является наиболее простым.

Пусть простая гармоническая возбуждающая сила:

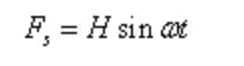
Где, H - амплитуда возбуждающей силы, ω - угловая частота возбуждающей силы.

Когда блок отклоняется от положения равновесия на расстояние x, дифференциальное уравнение движения блока имеет вид

Где, h=H/m, приведенное выше уравнение является дифференциальным уравнением вынужденных колебаний с одной степенью свободы с вязким демпфированием, которое представляет собой линейное неоднородное обыкновенное дифференциальное уравнение второго порядка с постоянным коэффициентом.

Приведенное выше уравнение полностью соответствует выражению реакции напряжения емкостной нагрузки, которое мы изучали в теории цепей и которое представляет собой линейное неоднородное обыкновенное дифференциальное уравнение второго порядка с постоянным коэффициентом.

Затухание в цепи зависит от сопротивления, потому что сопротивление только потребляет, но не накапливает энергию.

При простом гармоническом возбуждении общее решение дифференциального уравнения движения демпфированной системы имеет вид:

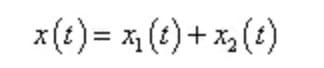
Где, x1 (t) - однородное решение, представляющее собой свободные затухающие колебания;

Из-за наличия демпфирования затухающая часть вибрации исчезает через определенный промежуток времени.

Решение этой задачи аналогично решению задачи о свободных колебаниях, поэтому здесь оно повторяться не будет.

Здесь мы рассматриваем специальное решение x₂ (t), генерируемой вынужденной вибрацией, которая может быть выражена как:

Среди них,

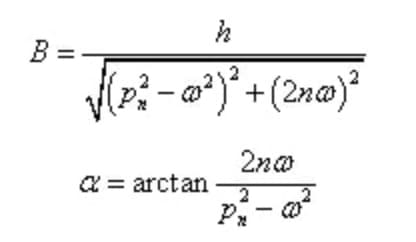
Амплитуда и сдвиг по фазе установившихся вынужденных колебаний не зависят от начальных условий, а зависят только от характеристик системы и возбуждения.

Установите соотношение частот, коэффициент демпфирования и коэффициент усиления амплитуды:

Приведенная выше формула может быть переписана как:

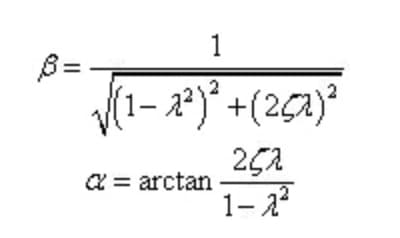
Исходя из этого, мы можем узнать реакцию системы при вынужденной вибрации.

Для лучшего понимания можно проиллюстрировать взаимосвязь между различными коэффициентами демпфирования, соотношениями частот и коэффициентами усиления амплитуды. Частота разделена на три области: низкочастотную, среднечастотную и высокочастотную. Как видно из рисунка, как в низкочастотной, так и в высокочастотной областях демпфирование оказывает минимальное влияние на коэффициент усиления амплитуды. Таким образом, демпфированная система может быть упрощена до уровня недемпфированной системы для упрощения расчетов.

Собственная и резонансная частота

Собственная частота - это неотъемлемая характеристика структурных свойств системы, определяемая исключительно ее массой и жесткостью и не зависящая от внешних факторов, таких как демпфирование. В системе с n степенями свободы существует n различных собственных частот, в то время как непрерывные системы обладают бесконечным числом собственных частот.

Резонанс возникает, когда частота внешнего возбуждения близко совпадает или совпадает с собственной частотой системы, заставляя структуру вибрировать со значительно увеличенной амплитудой. Это явление представлено синим кругом на сопроводительном рисунке. Резонансная частота, хотя часто приближается к собственной частоте в системах с легким демпфированием, может отклоняться от нее в конструкциях с сильным демпфированием, обычно оказываясь ниже собственной частоты.

При проектировании системы очень важно избегать не только конкретной резонансной пиковой частоты, но и окружающего резонансного диапазона, соответствующего промежуточной частотной области на рисунке. Эта мера предосторожности необходима, поскольку в этой полосе частот отклик системы значительно усиливается. Инженеры должны убедиться, что ни нормальная работа системы, ни внешние возбуждения от соседнего оборудования не попадают в этот критический диапазон.

Резонанс может иметь глубокие последствия, как благоприятные, так и пагубные. К негативным последствиям можно отнести обрушение подъемных балок, резонанс земли в вертолетах, повреждение оборудования и разрушение конструкций под воздействием инфразвука. И наоборот, резонанс намеренно используется в музыкальных инструментах для получения желаемых тонов и гармоник.

Чтобы снизить риски, связанные с резонансом, дизайнеры используют различные стратегии:

1. Настройка частоты: Настройка собственной частоты системы для выхода за пределы рабочего диапазона частот.
2. Усиление демпфирования: Включение материалов или механизмов для рассеивания колебательной энергии.
3. Усиление конструкции: Увеличение жесткости для изменения собственных частот и уменьшения амплитуды.
4. Виброизоляция: Внедрение систем, минимизирующих передачу внешних возбуждений.
5. Активное управление: Использование датчиков и исполнительных механизмов для борьбы с резонансными колебаниями в режиме реального времени.

Понимание и управление резонансом необходимо в самых разных областях - от гражданского строительства и аэрокосмической промышленности до точного производства и конструирования музыкальных инструментов. Передовые аналитические инструменты, такие как анализ методом конечных элементов и экспериментальный модальный анализ, играют решающую роль в прогнозировании и определении характеристик резонансного поведения сложных систем.