Вы когда-нибудь задумывались, почему одни материалы легко гнутся, а другие остаются жесткими? Этот блог погружается в увлекательный мир модуля упругости и жесткости, раскрывая их важнейшую роль в инженерии. В конце вы поймете, как эти свойства влияют на прочность и гибкость повседневных материалов.
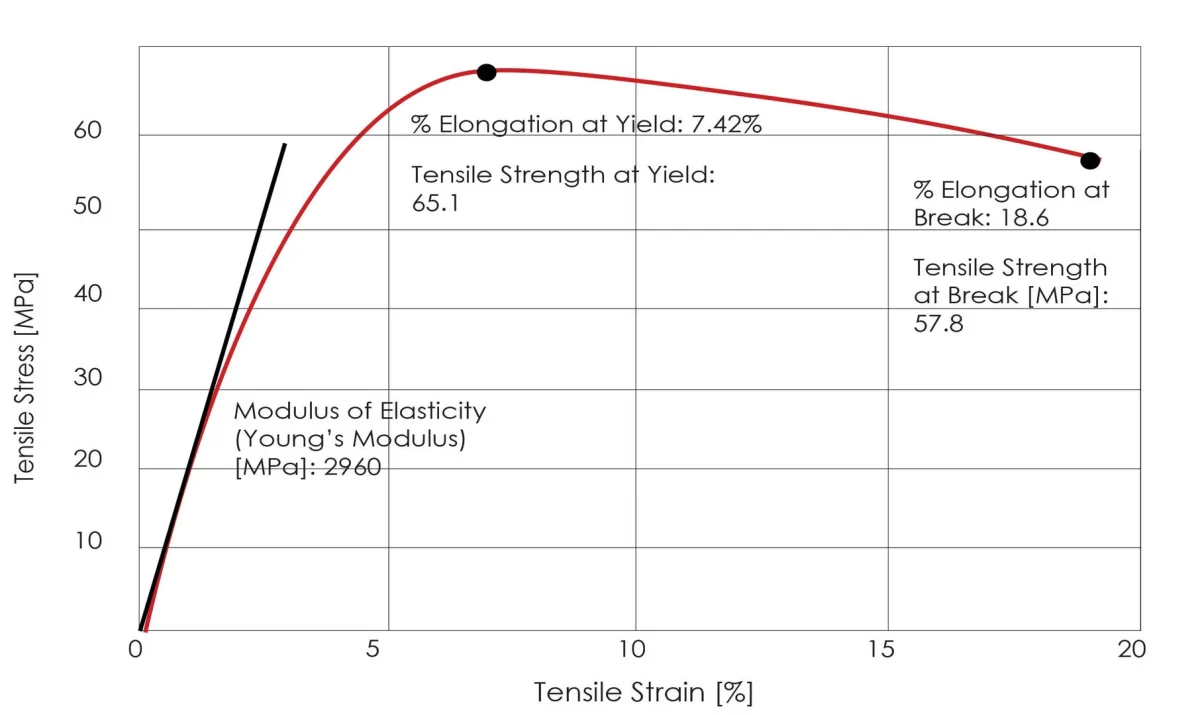
Модуль упругости: Отношение нормального напряжения к соответствующей нормальной деформации на стадии упругой деформации материала.
На стадии упругой деформации напряжение и деформация материала пропорциональны, в соответствии с законом Гука, а коэффициент пропорциональности называется модулем упругости.
Термин "модуль упругости" - это общее описание упругости материала. Он включает в себя несколько конкретных модулей, в том числе модуль Юнга, модуль сдвига, модуль объемной упругости и другие.
Поэтому термины "модуль упругости" и "модуль объемной упругости" являются инклюзивными.
Когда к эластомеру прикладывается внешняя сила (известная как "напряжение"), он изменяет свою форму (известную как "деформация"). Модуль упругости определяется как отношение напряжения к деформации.
Например:
Линейная деформация:
Когда к тонкому стержню прикладывается растягивающая сила F, линейное напряжение рассчитывается как отношение растягивающей силы к площади поперечного сечения S стержня.
Линейная деформация рассчитывается как удлинение стержня (dL), деленное на его первоначальную длину (L).
Линейное напряжение, деленное на линейную деформацию, равно модулю Юнга, E = (F / S) / (dL / L).
Деформация при сдвиге:
Когда к эластомеру прикладывается боковая сила (обычно сила трения) f, он меняет форму с квадратной на ромбовидную.
Этот угол деформации называется "деформацией сдвига", а соответствующая сила, деленная на площадь напряжения, - "напряжением сдвига".
Напряжение сдвига, деленное на деформацию сдвига, равно модулю сдвига, G = (f / S) / a.
Объемное растяжение:
Когда к эластомеру прикладывается общее давление P, оно называется "объемным напряжением".
Уменьшение объема эластомера (-dV), деленное на его первоначальный объем (V), называется "объемной деформацией".
Объемное напряжение, деленное на объемную деформацию, равно модулю объемной упругости, K = P / (-dV / V).
В общем случае, если нет путаницы, модуль упругости металлических материалов относится к модулю Юнга, также известному как положительный модуль упругости.
Единица измерения: E (модуль упругости) измеряется в ГПа.
Модуль упругости - важнейший эксплуатационный параметр инженерных материалов.
На макроуровне она измеряет способность объекта сопротивляться упругой деформации, а на микроуровне - отражает прочность связи между атомами, ионами или молекулами.
Факторы, влияющие на прочность связи, могут также влиять на модуль упругости материала, такие как режим связи, кристаллическая структура, химический состав, микроструктура, температура и другие.
Модуль Юнга металлические материалы может колебаться более чем на 5% из-за различных составов сплавов, состояний термообработки и холодных пластических деформаций.
Однако, как правило, модуль упругости металлические материалы это показатель механических свойств, нечувствительный к структуре.
Легирование, термообработка (структура волокон) и холодная пластическая деформация оказывают ограниченное влияние на модуль упругости, а внешние факторы, такие как температура и скорость нагружения, влияют на него незначительно.
Поэтому в инженерных приложениях модуль упругости считается постоянной величиной.
Единицы измерения: ГПа (гигапаскали) для модуля упругости.
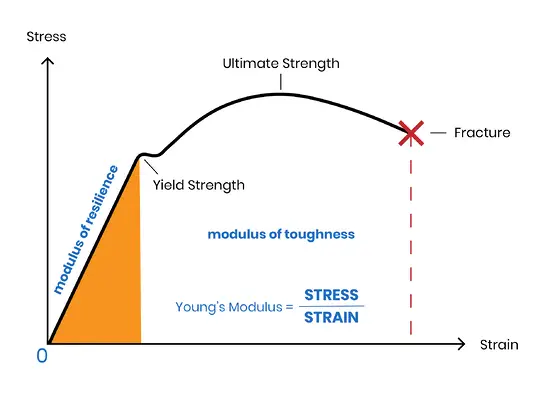
Модуль упругости - это показатель сопротивления материала упругой деформации.
Чем выше его значение, тем большее напряжение требуется для создания определенного объема упругой деформации, что означает, что материал более жесткий и испытывает меньшую упругую деформацию при заданном напряжении.
Модуль упругости, обозначаемый E, - это мера величины напряжения, необходимого для того, чтобы материал подвергся единичной упругой деформации под действием внешней силы.
Он представляет собой способность материала сопротивляться упругой деформации и может быть сравнен с жесткостью источник.
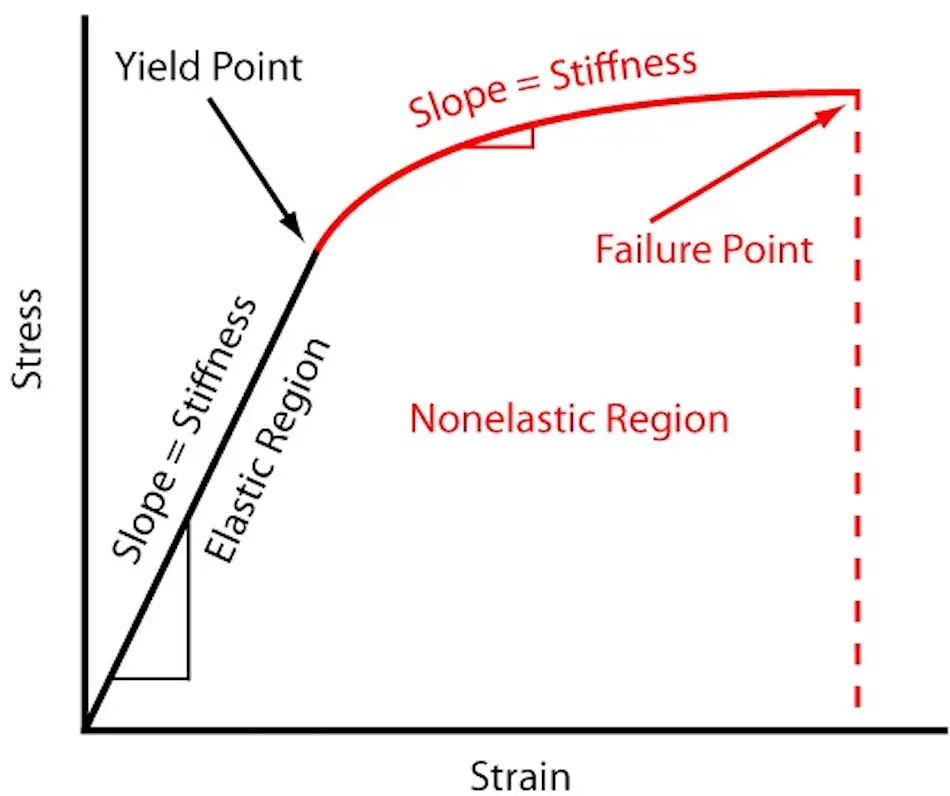
Жесткость" означает способность конструкции или компонента сопротивляться упругой деформации. Она определяется силой или моментом, необходимыми для создания единицы деформации.
Что касается вращательной жесткости, то она представлена символом "k" и может быть рассчитана как "k = M / θ", где "M" - приложенный момент, а "θ" - угол поворота.
Другие виды жесткости включают:
Метод расчета жесткости можно разделить на два подхода: теория малых перемещений и теория больших перемещений.
Теория больших перемещений учитывает деформацию конструкции после напряжения и соответствующим образом формирует уравнение равновесия, обеспечивая точные результаты, но с более сложным процессом расчета.
В отличие от этого, теория малых перемещений предполагает, что конструкция не подвергается значительным деформациям, поэтому внутренняя сила может быть получена из внешней нагрузки и затем использована для расчета деформации.
Этот подход широко используется в большинстве задач механического проектирования, поскольку он гораздо проще в решении.
Например, при расчете деформации изгиба балки часто используется теория малых перемещений, поскольку фактическая деформация очень мала.
Эта теория предполагает игнорирование первой производной прогиба в формуле кривизны и использование второй производной прогиба для аппроксимации кривизны оси балки, что позволяет упростить процесс решения за счет линеаризации дифференциального уравнения.
При одновременном действии нескольких нагрузок деформация изгиба, вызванная каждой нагрузкой, может быть рассчитана отдельно, а затем объединена.
Сопротивление деформации под действием статической нагрузки называется статической жесткостью, а сопротивление деформации под действием динамической нагрузки - динамической жесткостью, то есть величиной динамической силы, необходимой для получения единицы амплитуды.
Когда мешающая сила изменяется медленно (т.е. частота мешающей силы намного меньше частоты собственная частота конструкции), динамическая жесткость в основном равна статической жесткости.
Однако если мешающая сила изменяется быстро (т.е. частота мешающей силы намного больше собственной частоты конструкции), то деформация конструкции будет относительно небольшой, и, следовательно, динамическая жесткость будет относительно большой.
Если частота мешающей силы близка к собственной частоте конструкции, наступает резонанс, и динамическая жесткость становится минимальной, что делает конструкцию наиболее легко деформируемой, причем ее динамическая деформация может в несколько раз или даже более чем в десять раз превышать деформацию от статической нагрузки.
Чрезмерная деформация компонентов может повлиять на их работу.
Например, чрезмерная деформация вала шестерни может повлиять на зацепление шестерен, а чрезмерная деформация станка может снизить точность обработки.
К факторам, влияющим на жесткость, относятся модуль упругости материалов и форма конструкции. Изменение формы конструкции может оказать значительное влияние на жесткость.
Расчет жесткости является основой теории вибрации и анализа устойчивости конструкции. При неизменной массе высокая жесткость приводит к высокой собственной частоте.
Распределение напряжений в статически неопределимой конструкции связано с коэффициентом жесткости каждой детали.
На сайте механика разрушения Анализ позволяет определить коэффициент интенсивности напряжений в треснувшем элементе на основе его гибкости.
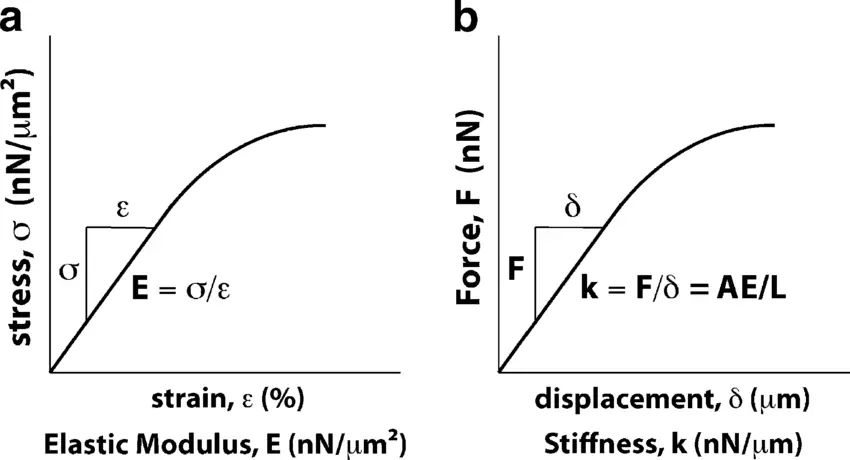
Жесткость и модуль упругости - фундаментальные понятия в материаловедении, каждое из которых описывает различные аспекты устойчивости материала к деформации. Хотя они связаны между собой, они играют разные роли в анализе и применении материалов.
Модуль упругости, также известный как модуль Юнга, является специфической мерой присущей материалу способности сопротивляться деформации под действием напряжения. Он определяет соотношение между напряжением (силой на единицу площади) и деформацией (пропорциональной деформацией) в линейной упругой области кривой "напряжение-деформация" материала. Модуль упругости является свойством материала и не зависит от его формы или размера. Он выражается в единицах давления, например, в паскалях (Па).
С другой стороны, жесткость - это более широкое понятие, обозначающее сопротивление конструкции упругим деформациям под действием приложенной нагрузки. Это не только свойство материала, но и зависимость от геометрии и граничных условий конструкции. Жесткость обычно выражается как сила, необходимая для достижения единичного перемещения (например, Ньютоны на метр, Н/м).
Жесткость элемента конструкции может быть определена на основе модуля упругости материала и геометрии элемента. Например, жесткость на изгиб (EI) балки - это произведение модуля упругости (E) и момента инерции (I) поперечного сечения балки. Аналогично, жесткость на кручение (GI) - это произведение модуля сдвига (G) и полярного момента инерции (I).
Жесткость имеет решающее значение при проектировании, особенно для компонентов, которые должны сохранять свою форму под нагрузкой, таких как шпиндели, направляющие и ведущие винты. Она также необходима для конструкций, требующих строгого контроля деформации, таких как крылья самолетов и высокоточные узлы.
Прочность - это способность материала сопротивляться постоянной деформации и разрушению под действием внешних сил. Она включает в себя различные виды прочности, в том числе предел текучести, предел прочности при растяжении, предел прочности при сжатии и предел прочности при изгибе. Эти свойства имеют решающее значение для определения несущей способности и долговечности механических деталей.
Понимание различий между жесткостью и модулем упругости необходимо для проектирования и анализа механических компонентов и конструкций. В то время как модуль упругости определяет внутреннее сопротивление материала деформации, жесткость учитывает как свойства материала, так и геометрические факторы, чтобы описать общее сопротивление конструкции деформации. Обе концепции являются неотъемлемой частью обеспечения работоспособности и надежности инженерных конструкций.
Как основатель MachineMFG, я посвятил более десяти лет своей карьеры металлообрабатывающей промышленности. Мой обширный опыт позволил мне стать экспертом в области производства листового металла, механической обработки, машиностроения и станков для обработки металлов. Я постоянно думаю, читаю и пишу об этих предметах, постоянно стремясь оставаться на переднем крае своей области. Позвольте моим знаниям и опыту стать преимуществом для вашего бизнеса.
RU 
EN 
DE 
ES 
FR 
IT 
NL 
PT 