В этой статье мы рассмотрим инновационные методы неразрушающего контроля, которые позволяют выявить истинный класс и прочность стальных конструкций. Узнайте, как ученые используют испытания на твердость и эмпирические формулы для обеспечения безопасности и надежности инженерных проектов. Окунитесь в мир науки и узнайте, что стоит за этими методами!
Точная оценка качества стальных конструкций, находящихся в эксплуатации, требует определения марки и прочности стали. Это является основой для надежных испытаний и оценки.
Традиционный метод определения прочности стали заключается в извлечении образцов из конструкции для испытания на растяжение, однако такой подход может нанести вред исходной конструкции и может быть нецелесообразным для некоторых конструкций.
Поэтому очень важно использовать неразрушающие методы контроля для расчета марки и прочности стали.
Исследователи как отечественные, так и зарубежные изучали методы неразрушающего контроля для определения прочности стали на инженерных объектах. В основном они сосредоточились на химическом составе и твердости и разработали несколько эмпирических формул.
Похожие статьи: Твердость металлов: Определенный справочник (с таблицей твердости)
Эти эмпирические формулы можно разделить на два типа:
Первый тип предполагает расчет прочности на растяжение на основе химического состава, как указано в формуле технического стандарта GB/T 50621-2010 для испытаний стальных конструкций на месте. Однако на прочность стальных материалов влияют химический состав и процесс производства (например, литье, ковка, прокатка и термообработка), поэтому расчет прочности стали только на основе химического состава может привести к значительному отклонению.
Второй тип предполагает расчет предела прочности на растяжение на основе твердости. Исследования показали, что существует положительная корреляция между твердостью и прочностью на разрыв стали. Прочность на разрыв прочность материалов может быть оценена по результатам испытаний на твердость, что является широко распространенным методом в инженерной практике.
В настоящее время основными отечественными стандартами, которые могут быть использованы для этой цели, являются GB/T 33362-2016 Conversion of Hardness Values of Металлические материалы и GB/T 1172-1999 Преобразование твердости и прочности черных металлов. GB/T 33362-2016 эквивалентен ISO 18265:2013 "Пересчет значений твердости металлических материалов". Сайт таблица пересчета твердости для нелегированной стали, низколегированной стали и литой стали в таблице A.1 настоящего стандарта были получены в результате сравнительных испытаний с проверенными и откалиброванными твердомерами в различных лабораториях Немецкой ассоциации инженеров-металлургов. GB/T 1172-1999 был получен в результате обширных испытаний и исследований, проведенных такими учреждениями, как Китайская академия метрологии. В таблице 2 этого стандарта приведены, в основном, коэффициенты пересчета, применимые к низкоуглеродистой стали.
Однако ни один из этих стандартов не предоставляет надежных данных со статистической значимостью для неопределенности значений пересчета, и диапазон отклонений результатов пересчета неизвестен. Исследователи изучили корреляцию между твердостью и прочностью стали, используемой в строительстве стальных конструкций, с помощью регрессионного анализа и сравнили ее с национальными стандартами, что служит проверкой и дополнением к стандартам GB/T 33362-2016 и GB/T 1172-1999. Они также обсудили метод обнаружения, подходящий для проектных площадок стальных конструкций, с использованием существующих портативных приборов для обнаружения.
Объектом исследования являются стальные листы Q235 и Q345, широко используемые при проектировании стальных конструкций.
Связанное чтение: Сталь Q235 против Q345
Для обеспечения репрезентативности образцов было отобрано 162 стальных листа от 86 производителей стальных конструкций в провинции Цзянсу, в том числе 82 листа из стали Q235 и 80 листов из стали Q345. Толщина стальных листов составляла 6, 8, 10, 12, 14, 18, 20 и 30 мм.
Стальные листы были обработаны в образцы полос 20 мм x 400 мм, и испытания на растяжение проводились на электрогидравлической сервомашине с микрокомпьютерным управлением, в соответствии с требованиями GB/T 228.1-2010.
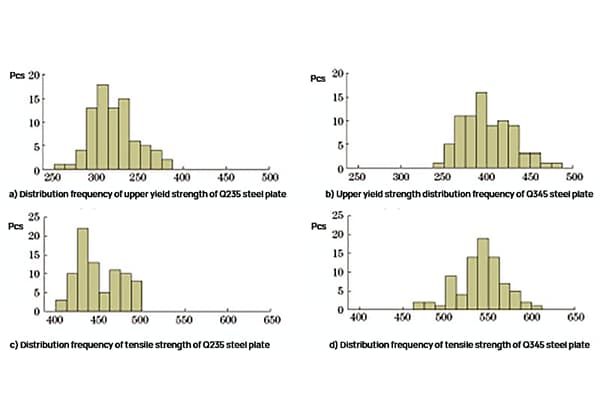
Результаты испытаний верхнего предел текучести и прочность на растяжение стальных листов Q235 и Q345 были подвергнуты статистическому анализу, частота распределения представлена на рисунке 1.
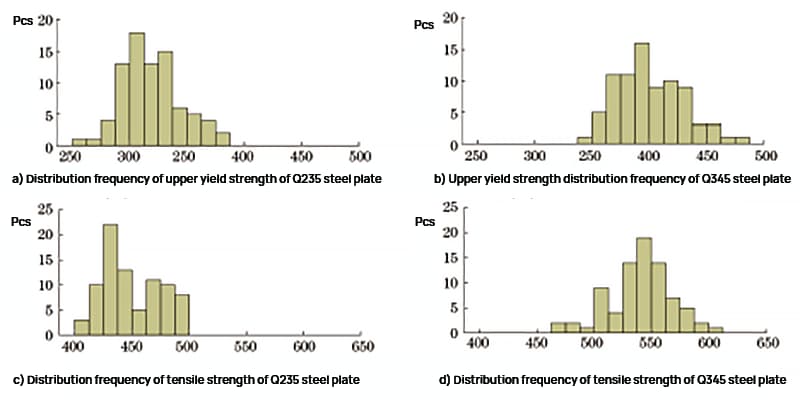
Рис. 1 Частота распределения прочности для Q235 Стальная пластина и стальной лист Q345
Как показано на рисунке 1, верхний предел текучести стального листа Q235 составляет от 261 до 382 МПа, а предел прочности при растяжении - от 404 до 497 МПа. Верхний предел текучести стального листа Q345 составляет от 345 до 477 МПа, а предел прочности при растяжении - от 473 до 607 МПа.
Распределение частот интенсивности примерно нормальное, а результаты испытаний соответствуют данным ежедневного осмотра, что говорит о высокой репрезентативности образцов.
Образцы для испытаний были отобраны и обработаны в соответствии с требованиями стандарта и прошли испытания на твердость по Роквеллу, твердость по Виккерсу, твердость по Бринеллю и растяжение.
Для проведения регрессионного анализа результатов испытаний на твердость и прочность использовался метод наименьших квадратов и программное обеспечение SPSS.
2.1.1 Результаты и анализ испытаний на твердость по Роквеллу
Поверхность образца была отшлифована с помощью шлифовальной машинки, чтобы убедиться, что она ровная и гладкая. Была выбрана шкала B, и прибор был откалиброван с помощью стандартного блока твердости. Испытание на твердость по Роквеллу проводилось в соответствии с требованиями стандарта GB/T 230.1-2018 Metallic Materials Rockwell Hardness Test Part 1: Test Method. Для каждого образца измеряли три точки и брали среднее значение.
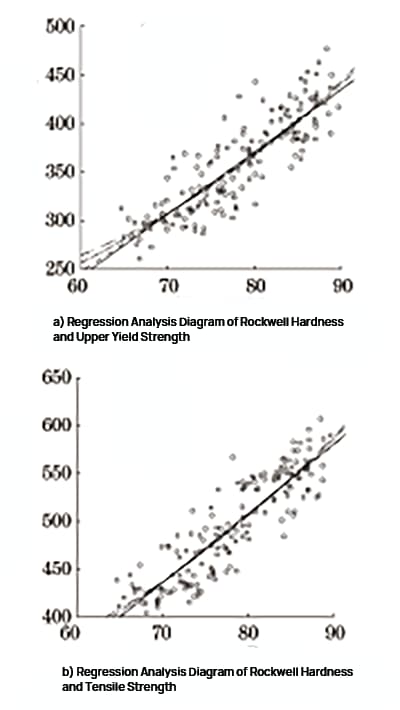
Рис. 2 Регрессионный анализ твердости и прочности по Роквеллу
С помощью программного обеспечения SPSS были проведены линейная регрессия, квадратичная регрессия, силовая регрессия и экспоненциальный регрессионный анализ твердости по Роквеллу, предела текучести и предела прочности при растяжении. Диаграмма регрессионного анализа представлена на рисунке 2, а результаты регрессионного анализа - в таблице 1 и таблице 2.
Таблица 1 Данные регрессионной модели твердости по Роквеллу и предела текучести
| Уравнение | Краткое описание модели | Параметр модели | ||||
| R2 | F | Значимость P | постоянная | b1 | b2 | |
| Линейная квадратичная экспонента | 0.736 | 446.897 | 0.000 | -143.077 | 6.426 | 0.081 |
| 0.741 | 227.290 | 0.000 | 341.852 | -6.141 | ||
| 0.740 | 456.461 | 0.000 | 0.828 | 1.392 | ||
| 0.744 | 464.965 | 0.000 | 86.806 | 0.018 | ||
Таблица 2 Данные регрессионной модели твердости по Роквеллу и прочности на разрыв
| Уравнение | Краткое описание модели | Параметр модели | ||||
| R2 | F | Значимость P | постоянная | b1 | b2 | |
| Линейная квадратичная экспонента | 0.780 | 565.900 | 0.000 | -71.394 | 7.241 | 0.074 |
| 0.783 | 286.412 | 0.000 | 372.980 | -4.274 | ||
| 0.778 | 560.887 | 0.000 | 3.477 | 1.137 | ||
| 0.782 | 574.207 | 0.000 | 155.315 | 0.015 | ||
Как видно из Таблицы 1 и Таблицы 2, твердость по Роквеллу имеет сильную корреляцию с прочностью, причем корреляция с пределом прочности на растяжение сильнее, чем с пределом текучести.
Из четырех регрессионных моделей между твердостью по Роквеллу и прочностью все имеют значимость P меньше 0,05 и близкое значение добросовестности соответствия R2.
Учитывая, что указанная в стандарте зависимость между твердостью по Роквеллу и прочностью на разрыв низкоуглеродистой стали похожа на полиномиальную модель, рекомендуется использовать квадратичную модель для преобразования.
Формула после подгонки такова:
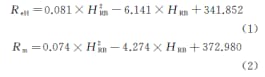
Где: ReH верхний предел текучести; Rm прочность на разрыв; HРБ твердость по Роквеллу.
2.1.2 Анализ относительных отклонений результатов преобразования
На основе модели квадратичной регрессии были рассчитаны и статистически проанализированы относительные отклонения между пересчитанными значениями верхнего предела текучести и предела прочности при растяжении и результатами испытания на растяжение. Объем выборки составил 162 человека, результаты представлены в таблице 3.
Относительные отклонения соответствуют нормальному распределению, а распределение частот показано на рисунке 3.
Таблица 3 Статистическая таблица относительного отклонения твердости по Роквеллу от прочности
| Статистические статьи | Минимальное значение | Максимальный | Среднее отклонение | Стандартная ссылка |
| Относительное отклонение значения преобразования верхнего предела текучести | -16.56 | +16.61 | ±5.46 | 6.84 |
| Относительное отклонение преобразованной прочности на разрыв | -13.31 | +11.16 | ±4.12 | 5.03 |
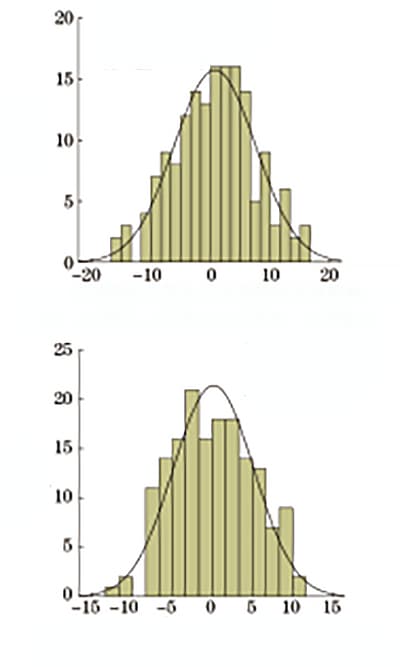
Рис. 3 Относительное отклонение твердости по Роквеллу от прочности
2.1.3 Сравнение с национальным стандартным значением пересчета
На рисунке 4 представлено сравнение значения преобразования прочности на разрыв, указанного в стандарте, значения преобразования, полученного по формуле квадратичной регрессии, и диаграммы рассеяния соответствующей зависимости между твердостью по Роквеллу и прочностью на разрыв, представленные на одном графике.

Рис. 4 Сравнительная диаграмма прочности на разрыв в пересчете на твердость по Роквеллу
Как видно из рисунка 4, общая тенденция трех кривых совпадает. Значение предела прочности на растяжение, приведенное в GB/T 1172-1999, аналогично данным автора, со средним отклонением 2,7% и максимальным отклонением 5,7% в диапазоне от 370 до 630 МПа.
Однако значение пересчета прочности на растяжение, приведенное в GB/T 33362-2016, ниже для стали Q235 (с прочностью на растяжение в диапазоне от 370 до 500 МПа) и выше для стали Q345 (с прочностью на растяжение в диапазоне от 470 до 630 МПа).
2.2.1 Процесс испытания на твердость по Виккерсу и анализ результатов
Поверхность образца была отполирована с помощью шлифовальной машинки, а прибор откалиброван с помощью стандартного блока твердости. Испытание на твердость по Виккерсу проводилось в соответствии с требованиями GB/T 4340.1-2009 Metallic Materials Vickers Hardness Test Part 1: Test Method. Для каждого образца измерялось три точки, и бралось среднее значение.
С помощью программного обеспечения SPSS были проведены линейная регрессия, квадратичная регрессия, силовая регрессия и экспоненциальный регрессионный анализ твердости по Виккерсу, верхнего предела текучести и предела прочности при растяжении. Диаграмма регрессионного анализа представлена на рисунке 5, а результаты регрессионного анализа - в таблице 4 и таблице 5.
Таблица 4 Данные регрессионной модели твердости по Виккерсу и предела текучести
| Уравнение | Краткое описание модели | Параметр модели | ||||
| R2 | F | Значимость P | постоянная | b1 | b2 | |
| Линейная квадратичная экспонента | 0.727 | 426.980 | 0.000 | -9.332 | 2.530 | 0.002 |
| 0.728 | 212.272 | 0.000 | 27.358 | 2.020 | ||
| 0.731 | 433.768 | 0.000 | 2.215 | 1.021 | ||
| 0.731 | 435.083 | 0.000 | 126.740 | 0.007 | ||

Рис. 5 Регрессионный анализ твердости и прочности по Виккерсу
Таблица 5 Данные регрессионной модели твердости по Виккерсу и прочности на разрыв
| Уравнение | Краткое описание модели | Параметр модели | ||||
| R2 | F | Значимость P | Постоянно | b1 | b2 | |
| Линейная квадратичная экспонента | 0.753 | 486.507 | 0.000 | 84.099 | 2.818 | 0.002 |
| 0.753 | 241.944 | 0.000 | 133.182 | 2.136 | ||
| 0.748 | 475.262 | 0.000 | 8.189 | 0.823 | ||
| 0.751 | 483.330 | 0.000 | 213.597 | 0.006 | ||
Как видно из табл. 4 и табл. 5, твердость по Виккерсу имеет сильную корреляцию с прочностью, причем корреляция с пределом прочности на растяжение сильнее, чем с пределом текучести.
Из четырех регрессионных моделей между твердостью по Виккерсу и прочностью все имеют значимость P меньше 0,05 и близкое значение добросовестности соответствия R2.
Учитывая, что указанная в стандарте зависимость между твердостью по Виккерсу и пределом прочности при растяжении низкоуглеродистой стали близка к линейной, рекомендуется использовать линейную зависимость для пересчета.
Формула после подгонки такова:

Где: HV твердость по Виккерсу.
2.2.2 Анализ относительных отклонений результатов преобразования
На основе модели линейной регрессии были рассчитаны и статистически проанализированы относительные отклонения между пересчитанными значениями верхнего предела текучести и предела прочности на разрыв и результатами испытания на разрыв. Объем выборки составил 162 человека, результаты представлены в таблице 6.
Относительные отклонения соответствуют нормальному распределению, а распределение частот показано на рисунке 6.
Таблица 6 Статистическая таблица относительного отклонения от твердости по Виккерсу к прочности
| Статистические статьи | Минимальное значение | Максимальный | Среднее отклонение | Стандартная ссылка |
| Относительное отклонение значения преобразования верхнего предела текучести | -19.30 | +17.55 | ±5.75 | 7.09 |
| Относительное отклонение преобразованной прочности на разрыв | -12.32 | +15.83 | ±4.88 | 5.44 |
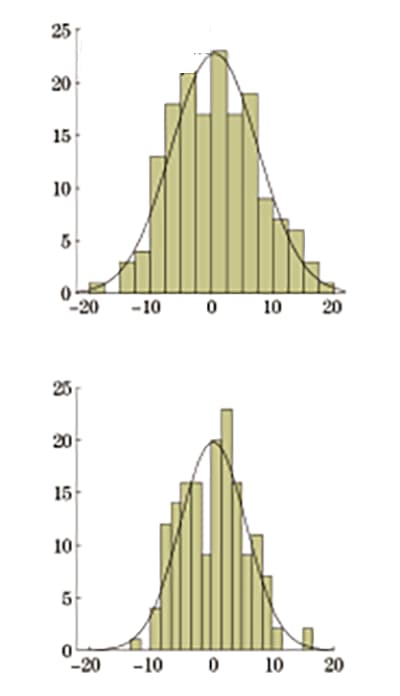
Рис. 6 Относительное отклонение твердости по Виккерсу в пересчете на прочность
2.2.3 Сравнение с национальным стандартным значением пересчета
На рисунке 7 представлено сравнение значения преобразования предела прочности на разрыв, указанного в стандарте, значения преобразования по формуле линейной регрессии, полученной автором, и диаграммы рассеяния соответствующей зависимости между твердостью по Виккерсу и пределом прочности на разрыв на одном графике.

Рис. 7 Сравнительная диаграмма прочности на разрыв в пересчете на твердость по Виккерсу
Как видно из рисунка 7, общая тенденция трех кривых совпадает. Значение пересчета прочности на растяжение, указанное в GB/T 1172-1999, очень близко к значению пересчета, полученному автором. В диапазоне от 370 до 630 МПа разница между ними немного увеличивается с ростом значения твердости, со средним отклонением в 1,2% и максимальным отклонением в 3,3%. Однако значение преобразования прочности на разрыв, приведенное в GB/T 33362-2016, в целом ниже.
2.3.1 Твердость по Бринеллю анализ процесса и результатов испытаний
Поверхность образца была отполирована с помощью шлифовальной машинки, чтобы обеспечить шероховатость поверхности не более 1,6 мкм. Прибор был откалиброван с помощью стандартного блока твердости, а испытание на твердость по Бринеллю проводилось в соответствии с требованиями GB/T 231.1-2018 Metallic Materials Brinell Hardness Test Part 1: Test Method. A цементированный карбид Использовался индентор диаметром 10 мм, а испытательное усилие составляло 29,42 кН. Для каждого образца измерялось три точки, и бралось среднее значение.
С помощью программного обеспечения SPSS были проведены линейная регрессия, квадратичная регрессия, силовая регрессия и экспоненциальный регрессионный анализ твердости по Бринеллю, верхнего предела текучести и предела прочности при растяжении. Диаграмма регрессионного анализа представлена на рисунке 8, а результаты регрессионного анализа - в таблице 7 и таблице 8.

Рис. 8 Регрессионный анализ твердости и прочности по Бринеллю
Таблица 7 Данные регрессионной модели твердости по Бринеллю и предела текучести
| Уравнение | Краткое описание модели | Параметр модели | ||||
| R2 | F | Значимость P | постоянная | b1 | b2 | |
| Линейная квадратичная экспонента | 0.756 | 495.403 | 0.000 | -59.965 | 2.846 | -0.001 |
| 0.758 | 246.186 | 0.000 | -86.188 | 3.205 | ||
| 0.757 | 497.365 | 0.000 | 1.048 | 1.168 | ||
| 0.756 | 494.881 | 0.000 | 110.318 | 0.008 | ||
Таблица 8 Данные регрессионной модели твердости по Бринеллю и прочности на разрыв
| Уравнение | Краткое описание модели | Параметр модели | ||||
| R2 | F | Значимость P | постоянная | b1 | b2 | |
| Линейная квадратичная экспонента | 0.887 | 1253.313 | 0.000 | -2.613 | 3.377 | -0.001 |
| 0.888 | 631.852 | 0.000 | -225.666 | 6.424 | ||
| 0.889 | 1286.205 | 0.000 | 3.204 | 1.009 | ||
| 0.886 | 1238.834 | 0.000 | 179.073 | 0.007 | ||
Как видно из Таблицы 7 и Таблицы 8, твердость по Бринеллю имеет сильную корреляцию с прочностью, причем корреляция с пределом прочности на разрыв сильнее, чем с пределом текучести.
Из четырех регрессионных моделей между твердостью по Бринеллю и прочностью все имеют значимость P меньше 0,05 и близкое значение добросовестности соответствия R2.
Учитывая, что конверсионные отношения между Твердость по Бринеллю углеродистой стали и прочности на разрыв, указанные в стандарте, близки к линейной зависимости, поэтому рекомендуется использовать линейную зависимость для преобразования.
Подходящая формула:

Где: HBW твердость по Бринеллю.
2.3.2 Анализ относительных отклонений результатов преобразования
В соответствии с полученной линейной регрессионной моделью рассчитываются относительные отклонения между преобразованными значениями верхнего предела текучести и предела прочности на разрыв и результатами испытаний на разрыв, и эти относительные отклонения подвергаются статистическому анализу.
Статистика равна 162, а результаты приведены в таблице 9.
Относительные отклонения имеют в основном нормальное распределение, а распределение частот показано на рис. 9.
Таблица 9 Статистическая таблица относительного отклонения от твердости по Бринеллю к прочности
| Статистические статьи | Минимальное значение | Максимальный | Среднее отклонение | Стандартная ссылка |
| Относительное отклонение значения преобразования верхнего предела текучести | -16.78 | +18.67 | ±5.38 | 6.75 |
| Относительное отклонение преобразованной прочности на разрыв | -9.25 | +8.55 | ±2.89 | 3.59 |

Рис. 9 Относительное отклонение твердости по Бринеллю в пересчете на прочность
2.3.3 Сравнение с национальным стандартным значением пересчета
В стандарте GB/T 1172-1999 отношение силы испытания к диаметру шарика индентора при испытании на твердость по Бринеллю составляет 10.
Авторское испытание проведено в соответствии с GB/T 231.1-2018. В соответствии с положениями стандарта, отношение силы испытания к диаметру шарика индентора составляет 30.
Таким образом, он больше не сравнивается с GB/T 1172-1999 в сравнении с национальным стандартом конверсионного значения.
Стандартное значение преобразования прочности на разрыв, приведенное в GB/T 33362-2016, значение преобразования по формуле линейной регрессии, установленной автором, и диаграмма рассеяния соответствующей зависимости между твердостью по Бринеллю и прочностью на разрыв сравниваются на одном графике, как показано на рис. 10.

Рис. 10 Сравнительная диаграмма прочности на разрыв в пересчете на твердость по Бринеллю
Из рис. 10 видно, что значение предела прочности при растяжении, приведенное в GB/T 33362-2016, практически совпадает с кривой регрессии предела прочности при растяжении, построенной автором, со средним отклонением 0,4% и максимальным отклонением 1,2% в пределах 370-630 МПа.
В последние годы быстрое развитие различных портативных твердомеров принесло большое удобство при проведении испытаний на месте.
В настоящее время на рынке можно приобрести множество типов портативных твердомеров по Роквеллу и портативных твердомеров по Бринеллю.
Оборудование портативно, просто в эксплуатации, быстро измеряет, а точность обнаружения соответствует требованиям национальных стандартов, что позволяет использовать его для обнаружения на объекте.
Существует также различное портативное оборудование для обработки образцов обработка поверхностичто может соответствовать требованиям испытаний.
Поэтому для расчета прочности стали при полевом обследовании металлоконструкций целесообразно использовать твердость по Роквеллу и твердость по Бринеллю.
| Твердость | Прочность на разрыв σb/МПа | ||||||||||||||||
| Rockwell | Поверхность по Роквеллу | Vickers | Бринелль | Углеродистая сталь | Хромистая сталь | Хромо-бариевая сталь | Хромоникелевая сталь | Хромомолибденовая сталь | Хромоникелевая молибденовая сталь | Хромо-марганцево-кремниевая сталь | Сверхвысокопрочная сталь | Нержавеющая сталь | Конкретный тип стали не указан | ||||
| HRC | HRA | HR15N | HR30N | HR45N | HV | HB30D2 | d10、2d5、4d2.5 /мм | ||||||||||
| 17 | – | 67.3 | 37.9 | 15.6 | 211 | 211 | 4.15 | 73.6 | 706 | 705 | 772 | 726 | – | 757 | – | 703 | 724 |
| 18 | – | 67.8 | 38.9 | 16.8 | 216 | 216 | 4.11 | 753 | 723 | 719 | 779 | 737 | – | 769 | – | 719 | 737 |
| 19 | – | 68.3 | 39.8 | 18 | 221 | 220 | 4.07 | 771 | 739 | 735 | 788 | 749 | – | 782 | – | 737 | 752 |
| 20 | – | 68.8 | 40.7 | 19.2 | 226 | 225 | 4.03 | 790 | 757 | 751 | 797 | 761 | – | 796 | – | 754 | 767 |
| 21 | – | 69.3 | 41.7 | 20.4 | 231 | 227 | 4 | 809 | 775 | 767 | 807 | 775 | – | 810 | – | 773 | 782 |
| 22 | – | 69.8 | 42.6 | 21.5 | 237 | 234 | 3.95 | 829 | 794 | 785 | 819 | 789 | – | 825 | – | 792 | 799 |
| 23 | – | 70.3 | 43.6 | 22.7 | 243 | 240 | 3.91 | 849 | 814 | 803 | 831 | 805 | – | 840 | – | 812 | 816 |
| 24 | – | 70.8 | 44.5 | 23.9 | 249 | 245 | 3.87 | 870 | 834 | 823 | 845 | 821 | – | 856 | – | 832 | 835 |
| 25 | – | 71.4 | 45.5 | 25.1 | 255 | 251 | 3.83 | 892 | 855 | 843 | 860 | 838 | – | 874 | – | 853 | 854 |
| 26 | – | 71.9 | 46.4 | 26.3 | 261 | 257 | 3.78 | 914 | 876 | 864 | 876 | 857 | 876 | 892 | – | 875 | 874 |
| 27 | – | 72.4 | 47.3 | 27.5 | 268 | 263 | 3.74 | 937 | 898 | 886 | 893 | 877 | 897 | 910 | – | 897 | 895 |
| 28 | – | 73 | 48.3 | 28.7 | 274 | 269 | 3.7 | 961 | 920 | 909 | 912 | 897 | 918 | 930 | – | 919 | 917 |
| 29 | – | 73.5 | 49.2 | 29.9 | 281 | 276 | 3.65 | 984 | 943 | 933 | 932 | 919 | 941 | 951 | – | 942 | 940 |
| 30 | – | 74.1 | 50.2 | 31.1 | 289 | 283 | 3.61 | 1009 | 967 | 959 | 953 | 943 | 966 | 973 | – | 966 | 904 |
| 31 | – | 74.7 | 51.1 | 32.3 | 296 | 291 | 3.56 | 1034 | 991 | 985 | 976 | 967 | 991 | 996 | – | 990 | 989 |
| 32 | – | 75.2 | 52 | 33.5 | 304 | 298 | 3.52 | 1060 | 1016 | 1013 | 1001 | 993 | 1018 | 1020 | – | 1015 | 1015 |
| 33 | – | 75.8 | 53 | 34.7 | 312 | 306 | 3.48 | 1086 | 1042 | 1042 | 1027 | 1020 | 1047 | 1046 | – | 1041 | 1042 |
| 34 | – | 76.4 | 53.9 | 25.9 | 320 | 314 | 3.43 | 1113 | 1068 | 1072 | 1054 | 1049 | 1077 | 1073 | – | 1067 | 1070 |
| 35 | – | 77 | 54.8 | 37 | 329 | 323 | 3.39 | 1141 | 1095 | 1104 | 1084 | 1079 | 1108 | 1101 | – | 1095 | 1100 |
| 36 | – | 77.5 | 55.8 | 38.2 | 338 | 332 | 3.34 | 1170 | 1124 | 1136 | 1115 | 1111 | 1141 | 1130 | – | 1126 | 1131 |
| 37 | – | 78.1 | 56.7 | 39.4 | 347 | 341 | 3.3 | 1200 | 1153 | 1171 | 1148 | 1144 | 1176 | 1161 | – | 1153 | 1163 |
| 38 | – | 78.7 | 57.6 | 40.6 | 357 | 350 | 3.26 | 1231 | 1184 | 1206 | 1132 | 1179 | 1212 | 1194 | – | 1184 | 1197 |
| 39 | 70 | 79.3 | 58.6 | 41.8 | 367 | 360 | 3.21 | 1263 | 1216 | 1243 | 1219 | 1216 | 1250 | 1228 | 1218 | 1216 | 1232 |
| 40 | 70.5 | 79.9 | 59.5 | 43 | 377 | 370 | 3.17 | 1296 | 1249 | 1282 | 1257 | 1254 | 1290 | 1264 | 1267 | 1250 | 1268 |
| 41 | 71.1 | 80.5 | 60.4 | 44.2 | 388 | 380 | 3.13 | 1331 | 1284 | 1322 | 1298 | 1294 | 1331 | 1302 | 1315 | 1286 | 1307 |
| 42 | 71.6 | 81.1 | 61.3 | 45.4 | 399 | 391 | 3.09 | 1367 | 1322 | 1364 | 1340 | 1336 | 1375 | 1342 | 1362 | 1325 | 1347 |
| 43 | 72.1 | 81.7 | 62.3 | 46.5 | 411 | 401 | 3.05 | 1405 | 1361 | 1407 | 1385 | 1379 | 1420 | 1384 | 1409 | 1366 | 1389 |
| 44 | 72.6 | 82.3 | 63.2 | 47.7 | 423 | 413 | 3.01 | 1445 | 1403 | 1452 | 1431 | 1425 | 1467 | 1427 | 1455 | 1410 | 1434 |
| 45 | 73.2 | 82.9 | 64.1 | 48.9 | 436 | 424 | 2.97 | 1488 | 1448 | 1498 | 1480 | 1472 | 1516 | 1474 | 1502 | 1457 | 1480 |
| 46 | 73.7 | 83.5 | 65 | 50.1 | 449 | 436 | 2.93 | 1533 | 1497 | 1547 | 1531 | 1522 | 1567 | 1522 | 1550 | 1508 | 1529 |
| 47 | 74.2 | 84 | 65.9 | 51.2 | 462 | 449 | 2.89 | 1581 | 1549 | 1597 | 1584 | 1573 | 1620 | 1573 | 1600 | 1563 | 1581 |
| 48 | 74.7 | 84.6 | 66.8 | 52.4 | 478 | 401 | 2.85 | 1631 | 1605 | 1649 | 1640 | 1626 | 1676 | 1627 | 1652 | 1623 | 1635 |
| 49 | 75.3 | 85.2 | 67.7 | 53.6 | 493 | 474 | 2.81 | 1686 | 1666 | 1702 | 1698 | 1682 | 1733 | 1683 | 1707 | 1688 | 1692 |
| 50 | 75.8 | 85.7 | 68.6 | 54.7 | 509 | 488 | 2.77 | 1744 | 1731 | 1758 | 1758 | 1739 | 1793 | 1742 | 1765 | 1759 | 1753 |
| 51 | 76.3 | 86.3 | 69.5 | 55.9 | 525 | 501 | 2.73 | – | 1803 | 1816 | 1821 | 1799 | 1854 | 1804 | 1827 | – | 1817 |
| 52 | 76.9 | 86.8 | 70.4 | 57.1 | 543 | – | – | – | 1881 | 1875 | 1887 | 1861 | 1918 | 1870 | 1894 | – | 1885 |
| 53 | 77.4 | 87.4 | 71.3 | 58.2 | 561 | – | – | – | – | 1937 | 1955 | 1925 | 1985 | 1938 | 1967 | – | 1957 |
| 54 | 77.9 | 87.9 | 72.2 | 59.4 | 579 | – | – | – | – | 2000 | 2025 | – | – | 2010 | 2045 | – | 2034 |
| 55 | 78.5 | 88.4 | 73.1 | 60.5 | 599 | – | – | – | – | 2066 | 2098 | – | – | 2086 | 2131 | – | 2115 |
| 56 | 79 | 88.9 | 73.9 | 61.7 | 620 | – | – | – | – | – | – | – | – | – | 2224 | – | 2201 |
| 57 | 79.5 | 89.4 | 74.8 | 62.8 | 642 | – | – | – | – | – | – | – | – | – | 2324 | – | 2293 |
| 58 | 80.1 | 89.8 | 75.6 | 63.9 | 664 | – | – | – | – | – | – | – | – | – | 2437 | – | 2391 |
| 59 | 80.6 | 90.2 | 76.5 | 65.1 | 688 | – | – | – | – | – | – | – | – | – | 2558 | – | 2496 |
| 60 | 81.2 | 90.6 | 77.3 | 66.2 | 713 | – | – | – | – | – | – | – | – | – | 2691 | – | 2607 |
| 61 | 81.7 | 91 | 78.1 | 67.3 | 739 | – | – | – | – | – | – | – | – | – | – | – | – |
| 62 | 82.2 | 91.4 | 79 | 68.4 | 766 | – | – | – | – | – | – | – | – | – | – | – | – |
| 63 | 82.8 | 91.7 | 79.8 | 69.5 | 795 | – | – | – | – | – | – | – | – | – | – | – | – |
| 64 | 83.3 | 91.9 | 80.6 | 70.6 | 825 | – | – | – | – | – | – | – | – | – | – | – | – |
| 65 | 83.9 | 92.2 | 81.3 | 71.7 | 856 | – | – | – | – | – | – | – | – | – | – | – | – |
| 66 | 84.4 | – | – | – | 889 | – | – | – | – | – | – | – | – | – | – | – | – |
| 67 | 85 | – | – | – | 923 | – | – | – | – | – | – | – | – | – | – | – | – |
| 68 | 85.5 | – | – | – | 959 | – | – | – | – | – | – | – | – | – | – | – | – |
| 69 | 86.1 | – | – | – | 997 | – | – | – | – | – | – | – | – | – | – | – | – |
| 70 | 86.6 | – | – | – | 1037 | – | – | – | – | – | – | – | – | – | – | – | – |
(1) Твердость по Роквеллу, твердость по Виккерсу и твердость по Бринеллю хорошо коррелируют с прочностью. На основе испытаний материалов получена формула преобразования твердости по Роквеллу, Виккерсу и Бринеллю в прочность, а относительное отклонение преобразования находится в допустимом диапазоне проекта.
Относительное отклонение между твердостью по Бринеллю и прочностью на разрыв явно меньше, чем между твердостью по Роквеллу и твердостью по Виккерсу.
(2) Предел прочности при растяжении в пересчете на твердость по Роквеллу, указанный в GB/T 33362-2016, является низким для стали Q235 и высоким для стали Q345.
Предел прочности при растяжении в пересчете на твердость по Виккерсу немного ниже.
Предел прочности при растяжении в пересчете на твердость по Бринеллю соответствует результатам испытаний.
Значения прочности на разрыв, пересчитанные по твердости Роквелла и Виккерса, приведенные в GB/T 1172-1999, близки к результатам испытаний.
(3) В сочетании с существующими портативными приборами для определения твердости и оборудованием для обработки образцов, использование твердости по Роквеллу и Бринеллю для расчета прочности стали может быть использовано в практических проектах и применено в инженерной практике.