Вы когда-нибудь сталкивались с проблемой точного раскладывания деталей из листового металла? В этой статье рассматриваются искусство и наука, лежащие в основе расчетов разворачивания листового металла. Откройте для себя ключевые понятия, формулы и методы, используемые опытными инженерами для точного разворачивания сложных геометрических форм. Узнайте, как применить эти принципы к собственным проектам и оптимизировать производственный процесс.
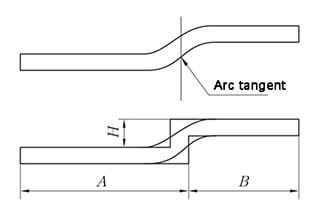
Первым шагом в процессе изготовления листового металла является развертка геометрических форм и цельного тела. Точность и правильность разворачивания образца напрямую влияет на качество конечной детали.
В прошлом, в связи с ограниченностью средств расчета, люди использовали метод проекции, увеличивая образец на плоскости с соотношением 1:1 и измеряя реальную длину требуемой линии плана.
Однако этот метод сложен и неэффективен и не может удовлетворить современные потребности производства.
С развитием вычислительных инструментов, таких как электронные калькуляторы и широкое распространение компьютеров, листовой металл Теперь разворачивание можно выполнять расчетными методами.
Чтобы стандартизировать метод расчета коэффициента разгибания листового металла техническими специалистами, минимизировать отклонения размеров изделий после гибки, а также облегчить самоконтроль персонала цеха и повторный контроль инспекторами качества, существует единый стандарт и основа для коэффициента разгибания.
В результате стандарт расчета коэффициента разворачивания листового металла становится все более стандартизированным.
Метод разворачивания нейтрального слоя
В процессе изгиба внешний слой испытывает растягивающее напряжение, а внутренний - сжимающее. Переходный слой между растягивающими и сжимающими напряжениями называется нейтральным слоем. Длина нейтрального слоя при изгибе остается такой же, как и до изгиба, что делает его эталоном для определения длины развернутой части гнутого изделия.
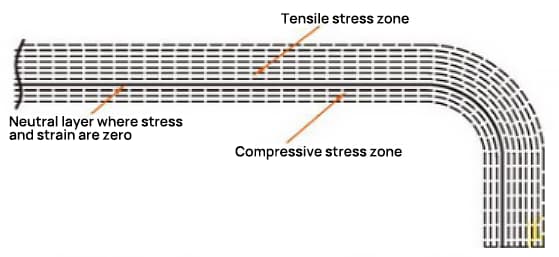
Расположение нейтрального слоя зависит от степени деформации.
Положение нейтрального слоя зависит не только от радиуса изгиба, толщины листа, коэффициента смещения внутрь и т.д., но и от таких факторов, как метод обработки, форма и размер листа.
Поэтому положение нейтрального слоя может быть определено лишь приблизительно, и в практических приложениях для расчетов обычно используются приблизительные значения.
Расчетная формула для размера длины L нейтрального слоя имеет вид:
Среди них,
Используя программное обеспечение 3D для моделирования и расчетов различных толщин, углов и радиусов, а также практику изготовления на месте, мы составили набор значений коэффициента K. Конкретные значения приведены в таблице 1.
Таблица 1: K-значения коэффициента нейтрального слоя
| р/т | ≤05 | 0.6 | 0.8 | 1 | 1.2 | 1.3 | 1.5 | 2 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | ≥8 |
| k | 026 | 0.28 | 0.30 | 0.32 | 0.33 | 0.34 | 0.36 | 0.38 | 0.39 | 0.4 | 0.42 | 0.44 | 0.46 | 0.5 |
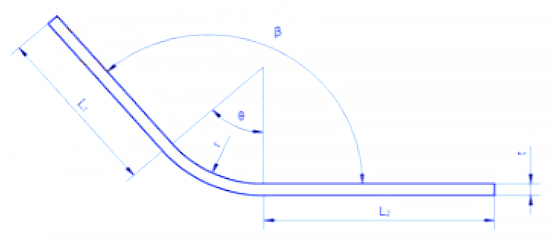
Расчет быстрого разворачивания для изгибов 90°
Схема разворачивания для изгиба на 90° показана на рис. 9. В последние годы для расчета размеров разгибания мы используем 3D-программы, такие как CATIA и SOLIDWORKS для моделирования листового металла.
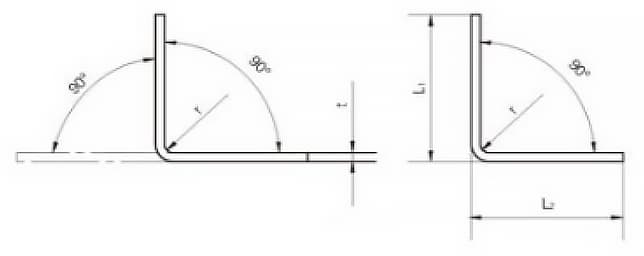
В результате многократных проверок было установлено, что при угле холодного изгиба плоского стального проката 90° формула для расчета развернутой длины L имеет следующий вид:
L = L1 + L2 - A
Где,
Таблица 2 Таблица параметров изгиба на 90°
| Толщина т/мм | Радиус настила r/мм | |||||||||||
| 1 | 1.2 | 16 | 2 | 25 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | |
| Компенсационное значение A мм | ||||||||||||
| 1 | -1.92 | -1.97 | -2.10 | -2.23 | -2.41 | -2.59 | -2.97 | -3.36 | -3.79 | -4.65 | -5.51 | -6.37 |
| 1.5 | -2.90 | -3.02 | -3.18 | -3.34 | -3.70 | -4.07 | -4.45 | -5.26 | -6.11 | -6.97 | ||
| 2 | -3.84 | -3.98 | -4.13 | -4.46 | -4.81 | -5.18 | -5.94 | -6.72 | -7.58 | |||
| 2.5 | -4.80 | -4.93 | -5.24 | -5.57 | -5.93 | -6.66 | -7.42 | -8.21 | ||||
| 3 | -5.76 | 6.04 | -6.35 | -6.69 | -7.40 | -8.14 | -8.91 | |||||
| 4 | -7.7 | -7.95 | -8.26 | -8.92 | -9.62 | -10.36 | ||||||
| 5 | -9.6 | -9.87 | -10.48 | -11.15 | -11.85 | |||||||
| 6 | -11.5 | -12.08 | -12.71 | -13.38 | ||||||||
| 8 | -15.4 | -15.9 | -16.51 | |||||||||
| 10 | -19.2 | -19.73 | ||||||||||
| 12 | 23.01 | |||||||||||
Когда радиус изгиба велика, а угол изгиба мал, степень деформации низкая, а нейтральный слой находится близко к центру толщины листа.
Однако, когда радиус изгиба (R) становится меньше и угол изгиба (θ) увеличивается, степень деформации также возрастает, и нейтральный слой перемещается к внутренней стороне центра изгиба. Расстояние от нейтрального слоя до внутренней стороны листа обозначается λ, а толщина материала - T.
Основная формула для расчета длины разворота:
Длина разворачивания = внутренний размер материала + внутренний размер материала + величина компенсации.
Вы также можете использовать следующий калькулятор для расчета длины разворота листового металла:

Далее описываются алгоритмы разворачивания различных элементов изгиба по очереди.
R = 0 мм, θ = 90° (Примечание: Если R ≤ 1,0 мм, то считается, что R = 0 мм).
L = A + B + K
В реальном производстве гибочный верхний штамп может иметь угол R, или угол R может быть меньше 1 мм, или выбор нижний штампV-образный паз может быть большим, что, помимо прочих причин, приводит к небольшому коэффициенту изгиба. В результате коэффициент изгиба для каждой толщины пластины материала представлен в таблице 1 на основе фактических эмпирических значений.
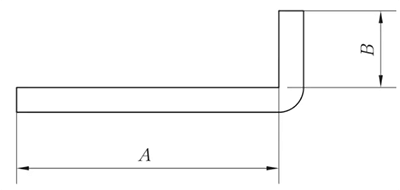
Рис. 1 Принципиальная схема общего изгиба I
R ≠ 0 мм и θ = 90°
L = A + B + K (K - длина дуги нейтрального слоя)
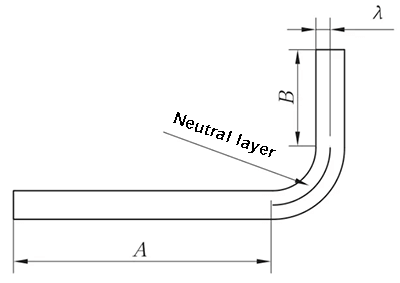
Рис. 2 Принципиальная схема общего изгиба II
R = 0 мм, θ ≠ 90°
L = A + B + K'
Примечание: K - величина компенсации при 90°.
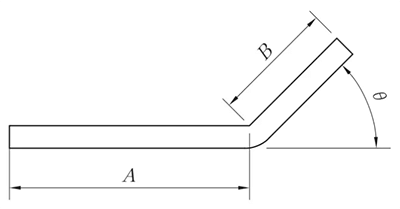
R ≠ 0 мм, θ ≠ 90°
L = A + B + K
(K - длина дуги нейтрального слоя)
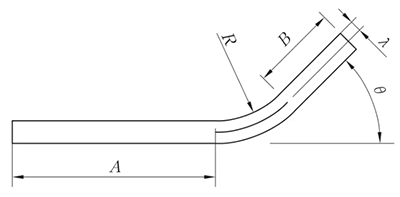
Рис. 4 Общий изгиб IV диаграмма изгиба
Метод разворачивания эквивалентен методу параллельного прямого Z-складывания, а измерение высоты показано на рисунке 6.
Угол θ считается разворотом на 90°.
Для 0 < T ≤ 1,6 мм, λ равна 0,5T.
Если T больше 1,6 мм, λ равна 0,4T.
Z-Fold, также называемый Сгибание со смещениемВ зависимости от угла формовки различают гибки со смещением по прямому краю и гибки со смещением по скошенному краю, а метод обработки определяется высотой смещения.
Когда высота смещения, h, меньше толщины материала в 3,5 раза, офсетные штампы или сменные штампы используются для формовки.
Если высота смещения превышает 3,5 толщины материала, используется обычное позитивное и негативное формование.
Если длина скошенной кромки меньше толщины материала в 3,5 раза, для формовки используются офсетные или сменные штампы.
Если длина скошенного края превышает толщину материала в 3,5 раза, применяется обычная однополюсная и одноотрицательная фальцовка.
(1) Когда H < 3,5T, только тогда можно обрабатывать с помощью гибки со смещением.
L = A + B + H
(если H ≤ T, то компенсируйте 0,2 мм)
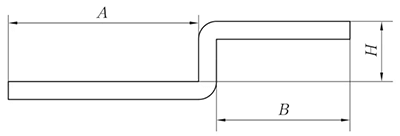
Рис. 5 Схема смещения прямой кромки
(2) Непараллельное прямолинейное смещение
Метод расширения такой же, как и метод параллельного прямого Z-складывания, а значение высоты показано на рисунке 6.
Угол θ можно считать развернутым на 90°.
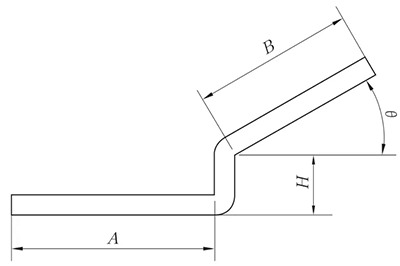
Рис. 6 Схема непараллельного смещения прямой кромки
(3) Смещение по прямой - переходный сегмент является касательной к двум дугам
При раскладывании материала с прямым смещением краев в точке касания двух круговых дуг на внешней поверхности подложки образуется вертикальная линия в точке касания двух круговых дуг. Затем материал смещается на одну толщину материала внутрь, как показано на рис. 7, для обработки и разворачивается с помощью метода Z-Fold 1 (Straight-Edge Offset).
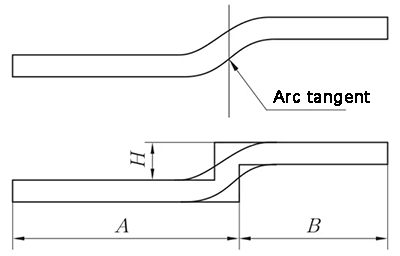
Рис. 7 Диаграмма смещения прямой кромки - переходный сегмент является касательной к двум дугам окружности
Когда H < 2T, алгоритм разворачивания в соответствии с обработкой смещения выглядит следующим образом.
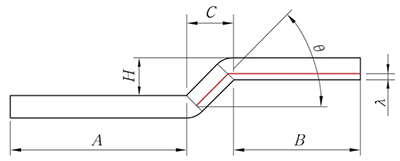
Рис. 8 Схема смещения скошенного края
L = A + B - K
(1) При сплющивании следует рассмотреть возможность прессования линии перед сгибанием в зависимости от фактических условий.
Место запрессовки линии находится в центре зоны деформации при изгибе.
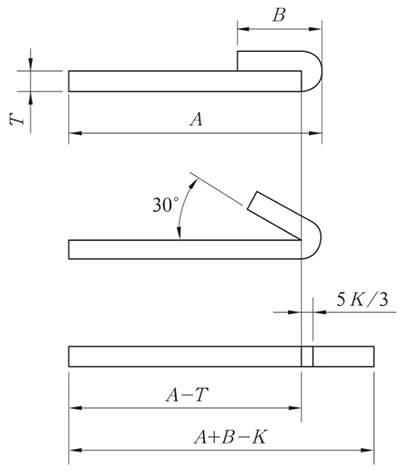
Рис. 9 Схема обратного складывания и сплющивания
Процессы обратного фальцевания и сплющивания обычно выполняются в два этапа: сначала материал сгибается на 30° с помощью вставного штампа, а затем сплющивается.
Поэтому при создании линия сгиба на развернутом чертеже необходимо проиллюстрировать линию сгиба, основанную на изгибе на 150°, как показано на рис. 9.
Таблица 1 Коэффициент изгиба пластин различной толщины при различных углах изгиба
| Угол | Толщина/мм | ||||
|---|---|---|---|---|---|
| 1 | 1.2 | 1.5 | 1.8 | 2.5 | |
| 45° | 5.3 | 6.3 | 7.8 | 9.5 | 13 |
| 50° | 4.5 | 5.4 | 6.8 | 8.1 | 11.25 |
| 55° | 4 | 4.7 | 5.8 | 7.05 | 9.75 |
| 60° | 3.4 | 4.1 | 5.1 | 6.15 | 8.5 |
| 65° | 3 | 3.6 | 4.5 | 5.4 | 7.5 |
| 70° | 2.65 | 3.2 | 4 | 4.75 | 6.6 |
| 75° | 2.35 | 2.8 | 3.5 | 4.25 | 5.9 |
| 80° | 2.1 | 2.5 | 3.1 | 3.75 | 5.25 |
| 85° | 1.9 | 2.25 | 2.8 | 3.35 | 4.65 |
| 90° | 1.7 | 2 | 2.5 | 3 | 4.15 |
| 95° | 1.5 | 1.8 | 2.2 | 2.7 | 3.75 |
| 100° | 1.35 | 1.6 | 2 | 2.4 | 3.35 |
| 105° | 1.2 | 1.4 | 1.75 | 2.15 | 3 |
| 110° | 1.1 | 1.3 | 1.6 | 2 | 2.65 |
| 115° | 1 | 1.25 | 1.4 | 1.7 | 2.35 |
| 120° | 0.85 | 1 | 1.25 | 1.5 | 2.1 |
| 125° | 0.75 | 0.9 | 1.1 | 1.35 | 1.85 |
| 130° | 0.65 | 0.8 | 1 | 1.18 | 1.65 |
| 135° | 0.55 | 0.7 | 0.85 | 1.05 | 1.45 |
| 140° | 0.5 | 0.6 | 0.75 | 0.9 | 1.25 |
| 145° | 0.43 | 0.5 | 0.65 | 0.77 | 1.05 |
| 150° | 0.35 | 0.43 | 0.55 | 0.65 | 0.9 |
| 155° | 0.3 | 0.35 | 0.45 | 0.53 | 0.75 |
| 160° | 0.23 | 0.27 | 0.35 | 0.4 | 0.6 |
| 165° | 0.17 | 0.2 | 0.25 | 0.3 | 0.45 |
Метод N-кратной обработки включает в себя как перестроение, так и сплющивание, а алгоритм разворачивания представляет собой:
L = A + B + K
(K - длина дуги нейтрального слоя).
λ = 0,5T
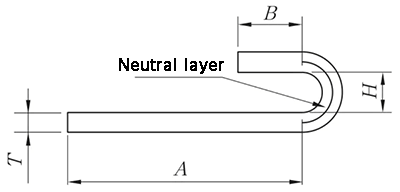
Рис.10 N-кратная диаграмма
(1) Расширение дуги непосредственно K, и берется длина дуги нейтрального слоя. λ= 0.5T
(2) Расширение с прямой кромкой с одной стороны.
L = A + K
(k - длина дуги нейтрального слоя)
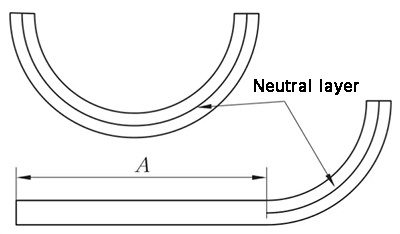
Рис. 11 Схематическая диаграмма дугового изгиба
В реальном производстве точный контроль длины развернутого металлического листа с помощью 3D-программ может быть достигнут в основном с помощью следующих шагов и методов:
Выберите подходящее программное обеспечение для 3D-проектирования: Во-первых, вам нужно выбрать программное обеспечение 3D CAD, подходящее для проектирования листового металла. SolidEdge, Creo, FreeCAD, UG и т. д. - это все программы, которые можно использовать для проектирования листового металла. В этих программах есть модули для листового металла или связанные с ними функции, которые могут помочь конструкторам в проектировании и расчетах раскладки деталей из листового металла.
Используйте модуль для работы с листовым металлом или инструменты в программном обеспечении: Большинство программных продуктов 3D CAD предоставляют соответствующие инструменты и функции для проектирования листового металла. Например, Creo предлагает различные методы контроля развернутых размеров листового металла, включая моделирование и разворачивание деталей из листового металла с большой дугой, метод вычитания изгибов и т. д. FreeCAD, как программное обеспечение для 3D-моделирования с открытым исходным кодом, также предоставляет модуль для работы с листовым металлом.
Приложениели разворачивающиеся методы расчета: Для обеспечения точности длины после разворачивания металлического листа можно использовать различные методы расчета разворачивания. К общим методам относятся метод компенсации изгиба, метод вычитания изгиба и метод расчета коэффициента K. Эти методы помогают конструкторам рассчитать фактическую длину материала в развернутом состоянии, обеспечивая тем самым ожидаемый размер деталей после окончательной гибки и формовки.
Уделите внимание обработке краев и углов и настройке деталей: В процессе проектирования листового металла очень важны детали обработки кромок и углов. Некоторые программы, например SW, предлагают различные решения по обработке кромок и углов и методы гибки, что помогает повысить точность раскладки.
Для изгибов не под 90 градусов распространенными углами изгиба являются, в частности, 45 и 135 градусов. Метод расчета коэффициента K основан на соотношении между толщиной материала и радиусом изгиба.
В частности, коэффициент K = δ / T, где δ - толщина материала, а T - радиус изгиба. Этот метод применим для расчета коэффициента изгиба любого угла, не равного 90 градусам.
В практических приложениях из-за возможных различий и больших погрешностей в значениях вычетов для изгибов под разными углами в качестве коэффициента изгиба обычно используется коэффициент K.
Кроме того, для точного определения значения коэффициента K для листов различной толщины необходимо вносить коррективы. По некоторым данным, значение коэффициента K для любого радиуса изгиба может быть рассчитано с помощью специальных методов интерполяции, которые доказали свою эффективность при использовании листового металла в промышленности.
Формула расчета увеличенной длины скошенного листового металла для пресса-тормоза имеет вид: [L = A + B + C + 0,2], где (A), (B) и (C) представляют собой внутренние размеры, а 0,2 служит в качестве компенсационной величины.
Основанная на общих принципах и практике расчетов расширения листового металла, эта компенсационная величина учитывает расхождения между фактической и теоретически рассчитанной длиной, вызванные такими факторами, как изгиб материала и погрешности точности пресс-формы во время реальных операций.
При обработке листового металла эта компенсационная величина помогает обеспечить точность размеров и качество конечного продукта.
Детали из листового металла широко используются в электромеханической, легкой и автомобильной промышленности.
Развернутая форма деталей из листового металла является основным фактором, определяющим размер заготовки, который, в свою очередь, влияет на размер и форму заготовки.
Однако традиционные методы разворачивания деталей из листового металла становятся все более неадекватными для удовлетворения потребностей современного дизайна из-за их длительных циклов, низкой эффективности и низкого качества.
Для устранения этих недостатков в последние годы все чаще используются передовые системы автоматизированного проектирования.
Эти специализированные системы проектирования деталей из листового металла обладают широкими функциональными возможностями и позволяют значительно сократить время и усилия, необходимые для предварительного проектирования и создания деталей из листового металла.