Что, если бы вы могли с легкостью и точностью выполнять сложные Z-образные изгибы в металле? Эта статья посвящена структурным нюансам Z-образной гибки и штампа для формовки, в ней представлены основные методы и расчеты. Вы узнаете, как оптимизировать процессы гибки, понять распределение напряжений и использовать композитные штампы для различных листовых материалов. Независимо от того, инженер вы или механик, вы получите знания, которые помогут вам оптимизировать производство и повысить точность ваших проектов по металлообработке. Погрузитесь в курс дела, чтобы овладеть сложностями Z-образной гибки и улучшить свой рабочий процесс.
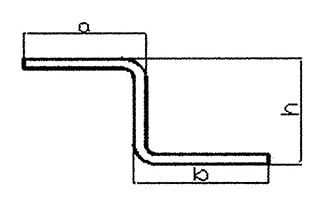
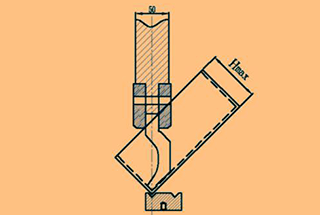
Z-образная гибочная заготовка, показанная на рис. 1, - часто встречающаяся в производстве деталь. Размер h ограничен нижним штампом, а минимальный размер, который может быть согнут существующим нижним штампом, приведен в таблице 1.
Таблица 1 Минимальный размер изгиба
| Толщина пластины | 1 | 1.5 | 2 | 2.5 | 3 |
| Минимальный размер | 7 | 9.5 | 14 | 16 | 18 |
В практическом производстве, если имеется множество Z-образных гибочных штампов, размер которых меньше указанного, потребуется разработать составной гибочный штамп для осуществления первичного формования. Этот составной штамп можно использовать для сгибания Z-образных гибочных штампов различных размеров на различных листовых материалах.
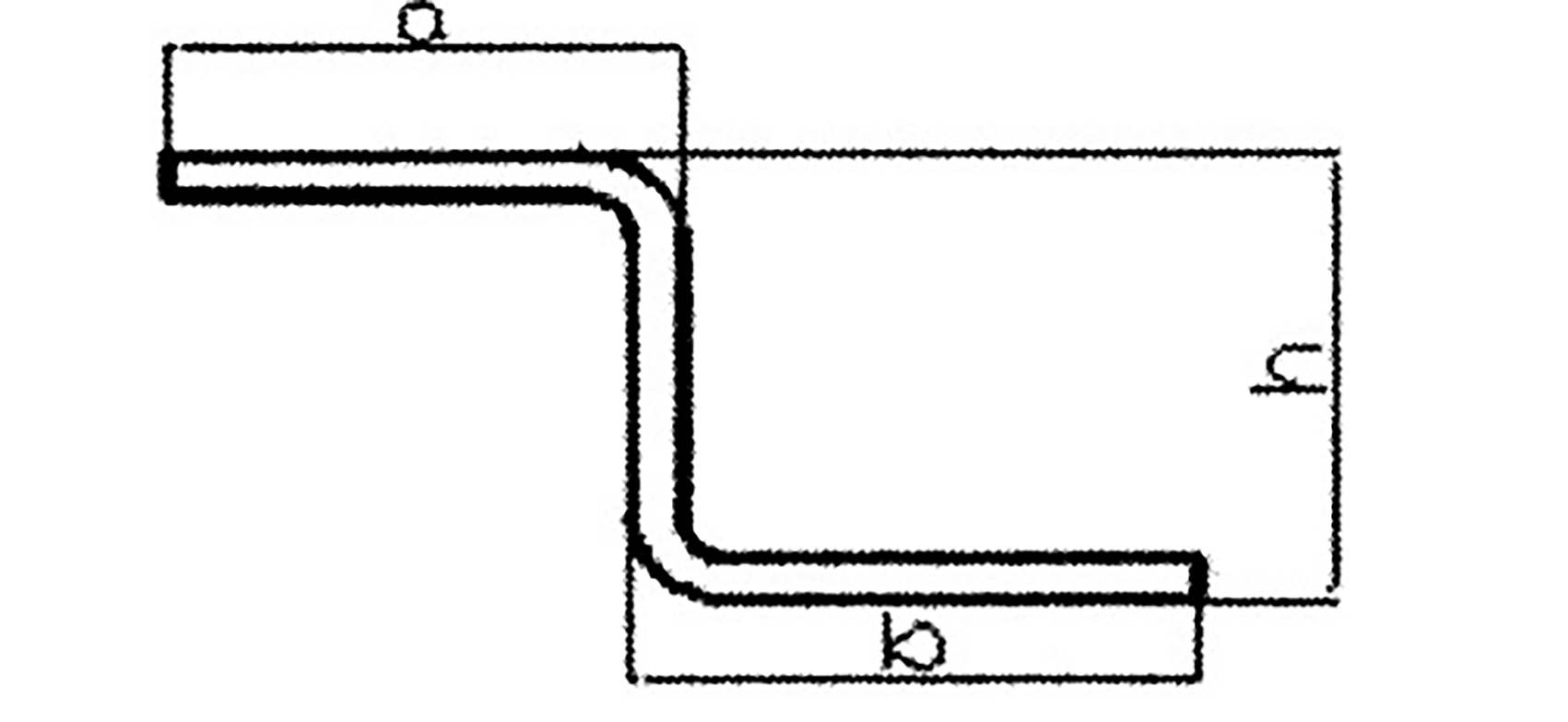
Рис. 1 Z-образный гибочный штамп
Рис. 2 Диаграмма сил воздействия
Как показано на рисунке 2, когда листовой металл при изгибе испытывает изгибающий момент, сдвигающую силу и местное давление. Однако основным фактором деформации при изгибе является изгибающий момент.
Приложение внешней силы приводит к соответствующей деформации металлического листа, что также вызывает появление внутренней силы, противостоящей деформации. Внутренняя сила уравновешивает внешнюю силу и измеряется как напряжение, которое представляет собой внутреннюю силу на единицу площади объекта. Чем больше внешняя сила, тем больше напряжение и деформация.
Когда внешнее напряжение материала ниже предела упругости, металлический лист находится в состоянии упругой деформации. Согласно закону Гука, линейная зависимость между напряжением и деформацией на участке обусловлена линейным изменением расстояния между деформацией и центральным слоем (удлинение внешнего слоя и укорочение внутреннего).
Если внешняя сила снимается, металлический лист возвращается к своей первоначальной форме. Однако если внешняя сила продолжает расти, степень деформации изгибаемой части будет увеличиваться до тех пор, пока напряжение, вызванное внешней силой, не сравняется с пределом текучести материала, что приведет к пластической деформации внешнего материала.
По мере увеличения внешней силы пластическая деформация развивается от поверхности к центру. После снятия внешней силы упругая деформация немедленно исчезает, но пластическая деформация остается и приводит к постоянной деформации изгиба.
Если напряжение, вызванное внешним воздействием, превышает предел прочности материала, металлический лист подвергается разрушению в результате пластической деформации. Внутреннее сжатие во время гибка листового металла также приводит к пластической деформации, но этот тип пластической деформации увеличивает напряжение на поверхности, не вызывая повреждений, и поэтому часто игнорируется.
Теперь мы внимательно наблюдаем за пластической деформацией при изгибе.
Под действием изгибающего момента на участке пластины имеются три равные линии: ab= a1b1 = a2b2.
После изгиба внутренний слой укорачивается, а внешний удлиняется, то есть ab < a1b1 < a2b2.
Поэтому при изгибе внутренний материал подвергается сжатию и становится короче, а внешний материал растягивается и удлиняется.
Между растяжением и сжатием находится слой материала, который не испытывает ни растяжения, ни сжатия и называется нейтральным слоем. Этот слой остается неизменным по длине, не удлиняется и не укорачивается.
Процесс расчета изгибаемой части включает в себя разделение ее на несколько основных геометрических элементов, включая отрезки прямых линий и дуг. Длина каждого элемента рассчитывается отдельно, а общая длина всех элементов - это развернутая длина изгибаемой части.
Z-образная изгибаемая часть на рисунке 1 может быть разделена на пять частей, как показано на рисунке 2. Блоки 1, 3 и 5 представляют собой отрезки прямых линий, а блоки 2 и 4 - отрезки дуг.
Как уже говорилось ранее, слой волокна с постоянной длиной посередине до и после изгиба называется нейтральным слоем. При расчете длины расширения сегмента дуги фактически рассчитывается длина нейтрального слоя сегмента дуги.
Положение, x, нейтрального слоя с внутренней стороны дуги (как показано на рис. 3) обычно определяется соотношением r/t.
x = kt
Где:
Где:
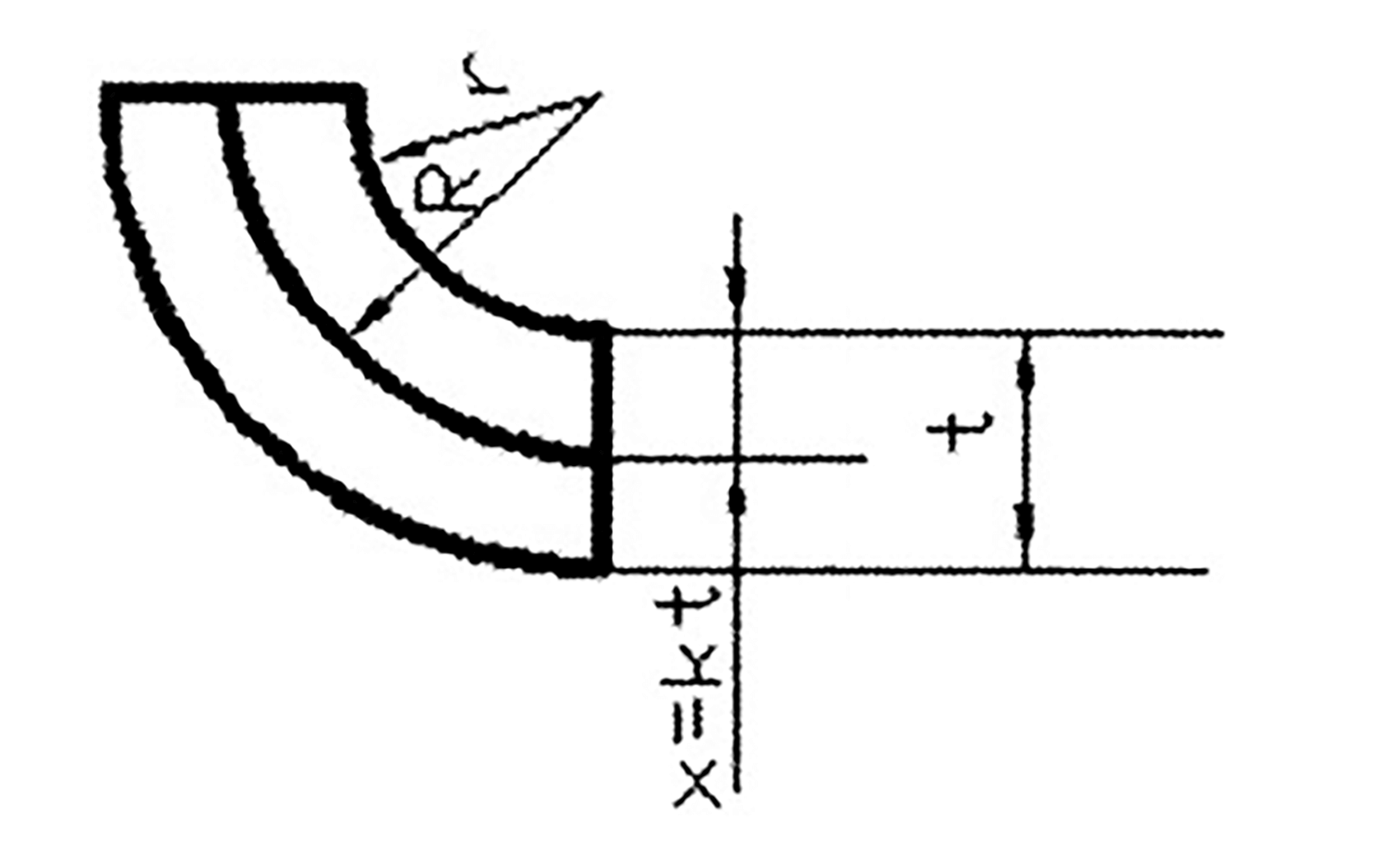
Рис. 3
Значение k меняется в зависимости от соотношения внутреннего радиуса и толщины листа, как показано в таблице 2:
Таблица 2
| р/т | 0.25 | 0.5 | 1 | 2 | 3 | 4 |
| k | 0.26 | 0.33 | 0.35 | 0.375 | 0.4 | 0.415 |
В практическом производстве чаще всего приходится сгибать стальные листы под углом 90 градусов.
Расчет длины дуги для 90-градусного изгиба с различными значениями r и t может быть получен с помощью таблиц в практических приложениях.
В данной статье рассматривается изгиб под прямым углом 90 градусов, однако неэффективно рассчитывать прямые и дуговые отрезки отдельно для деталей с углом 90 градусов. гибка листового металла. Вместо этого они обозначаются, как показано на рисунке 1.
При расчете материала для раскладывания мы можем использовать непосредственно обозначенные размеры, чтобы упростить процесс расчета.
Согласно рисунку 1, рассчитывается длина разработанного материала:
L = a+b+h - 2x
Где:
Таблица 3 Общий коэффициент изгиба x
| Толщина пластины t | Внутренний радиус изгиба r | |||
|---|---|---|---|---|
| 1.0 | 1.5 | 2.0 | 2.5 | |
| 0.5 | 1.0 | 1.2 | 1.4 | 1.6 |
| 1 | 1.9 | 2.1 | 2.3 | 2.5 |
| 1.5 | 2.5 | 2.7 | 2.9 | 3.1 |
| 2.0 | 3.4 | 3.6 | 3.8 | 4.0 |
| 2.5 | 4.0 | 4.2 | 4.4 | 4.6 |
| 3 | 4.9 | 5.1 | 5.3 | 5.4 |
Этот простой наборный штамп отличается от обычного штампа.
Он разработан для того, чтобы быть простым, быстрым, легко обрабатываемым и легко формируемым. Хотя он может быть не таким точным, как обычный штамп, он все равно используется для быстрой и точной обработки изделий.
Схема формовки композитного штампа приведена в таблице 3.
Принцип обработки: Толщина прокладки регулируется для достижения необходимой ширины V-образного паза в верхней и нижний штампи выполнить однократную обработку Z-складки под давлением.
Структура штампа: Z-образный гибочный штамп состоит из верхнего штампа, нижнего штампа, прокладки и стальной угловой призмы.
Толщина прокладки: Прокладка изготовлена из 0.Толщина 5 мм Сталь и укладывается в штабель для достижения необходимой толщины.
Стальная призма: Прямоугольная стальная деталь внутри матрицы, четыре угла которой имеют фаски со сторонами 0,5 мм, 1,0 мм, 2,0 мм и 4,0 мм, как показано в таблице 3.
Специальный простой штамп используется для достижения желаемой ширины V-образного паза верхнего и нижнего штампа путем регулировки размера угловой призматической стали и толщины прокладки, а затем выполняет обработку Z-образного фальца на одном прессе.
Этот метод выбран из-за возможности увеличить V-образный паз и уменьшить образование складок, поэтому для пластин разной толщины требуются разные штыри, как показано в таблице 4.
Таблица 4
| Толщина пластины | t<0.8 | 0.8<t<1.0 | 1.0<t<1.2 | 1.2<t1.5 | t>1.5 |
| Штырь | 0.5 | 1.0 | 1.0 или 2.0 | 2.0 | 4.0 |
Метод отладки Z-образного гибочного штампа:
1) Оба сгиба прямой Z-складки составляют 90°. Расстояние между двумя кончиками инструмента составляет: 1.414/2×h;
2) Если складки на заготовке слишком глубокие, то необходимо выбрать большой угол.
b: накладка из железа; c: увеличение угла R;
3) Если высота достигнута, но угол больше 90°, то a: эксцентриситет штампа.
b: Увеличьте толщину прокладки;
4) Если две стороны Z-складки не параллельны, этого можно добиться путем увеличения или уменьшения толщины подкладки.
Если верхний сгиб превышает 90°, необходимо увеличить толщину нижнего штампа; а если нижний сгиб превышает 90°, необходимо увеличить толщину верхнего штампа.
Метод расчета расширения Z-образного изгиба:
Когда h > нормального размера сгиба, он должен разворачиваться в два сложения.
L=a + b + h - 2x
Где:
Когда h < нормального размера гибки, она расширяется путем одноступенчатой формовки.
L = a + B + h - 1,5x
Где:
Одна из эмпирических формул, применяемых на практике, заключается в вычитании 1,5x из общего размера одной пресс-формы.