Springs are widely used in both the mechanical and electronic industries due to their elastic properties.
When a spring is subjected to a load, it undergoes significant elastic deformation, transforming mechanical work or kinetic energy into stored deformation energy.
Upon unloading, the spring returns to its original state, with the stored deformation energy being converted back into mechanical work or kinetic energy.
The relationship between the spring load and its deformation is referred to as spring stiffness. The higher the stiffness, the stiffer the spring becomes.
1. Function of spring
The functions of springs include:
- Cushioning and damping, such as the damping springs used in car and train suspensions, and various buffer systems.
- Controlling the movement of mechanisms, such as valve springs in internal combustion engines and control springs in clutches.
- Storing and releasing energy, such as clock springs and gun latch springs.
- Measuring force, such as springs in spring scales and dynamometers.
2. Classification of springs
Springs can be categorized based on their stress nature into four types: tension springs, compression springs, torsion springs, and bending springs.
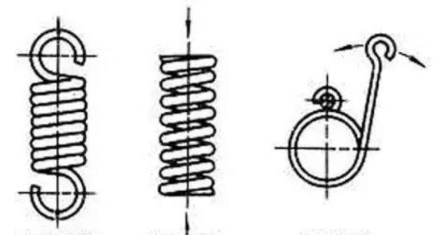
A tension spring is a type of coil spring that experiences axial tension.
These springs are typically made from circular cross-section materials.
When not subjected to a load, the coils of a tension spring are usually tightly coiled with no gaps between them.
A compression spring is a type of helical spring that is designed to withstand compressive forces.
The cross-section of compression springs is typically circular, but they can also be made from rectangular or multi-strand steel.
These springs usually have equal pitch, and there is a small space between the coils.
When subjected to an external load, the compression spring compresses, deforms, and stores energy in its deformation.
Torsion springs are a type of coil spring.
They are capable of storing and releasing angular energy, or of maintaining a device in a static position by rotating the force arm around the central axis of the spring body.
The ends of a torsion spring are fixed to other components, and when these components rotate around the center of the spring, the spring pulls them back to their original position, generating torque or rotational force.
In addition to the common types of springs, there are also two unconventional types: air springs and carbon nanotube springs.
An air spring is a non-metallic spring that utilizes the compressibility of air to create an elastic effect by adding pressurized air into a flexible enclosed container.
When used in high-end vehicle suspension systems, air springs greatly enhance ride comfort, making them widely used in automobiles and railway locomotives.
A carbon nanotube spring is created by spinning technology, starting with the preparation of a carbon nanotube film.
With a diameter of hundreds of microns and a length of a few centimeters, carbon nanotube springs have numerous potential applications including retractable conductors, flexible electrodes, micro strain sensors, supercapacitors, integrated circuits, solar cells, field emission sources, energy dissipation fibers, and more. They are also expected to be used in medical devices, such as tension sensing bandages.
3. Spring material and allowable stress
During operation, springs are often subjected to alternating and impact loads, and are required to undergo significant deformation. As a result, the material used to make springs should have high tensile strength, elastic limit, and fatigue strength.
Additionally, the manufacturing process should result in sufficient hardenability, resistance to decarburization, and good surface quality.
Common spring materials and allowable shear stress
| Material Science | See shear stress [τ] / MP for details | Shear modulus of elasticity G / MPa | Recommended operating temperature / ℃ | |||
|---|---|---|---|---|---|---|
| category | Code | Type I spring | Type II spring | Type III spring | ||
| Carbon spring steel wire | Group I II, II and III | 0.3s | 0.45 | 0.5 | 80000 | -40~120 |
| 65Mn | 420 | 560 | 700 | 80000 | -40~120 | |
| Alloy spring steel wire | 60Si2Mn | 480 | 640 | 800 | 80000 | -40~200 |
| 65SiMnWA | 570 | 760 | 950 | 80000 | -40~250 | |
| 50CrVA | 450 | 600 | 750 | 80000 | -40~210 | |
| Stainless steel wire | 1Cr18Ni9 | 330 | 440 | 550 | 73000 | -250~300 |
| 4Cr13 | 450 | 600 | 750 | 77000 | -40~300 | |
Note:
- Springs can be classified into three categories based on the number of cycles they undergo under load: Type I, with n > 106; Type II, with n = 103 ~ 105 and under impact load; and Type III, with n < 103.
- The allowable stress for shackle tension springs is 80% of the value listed in the table. If the spring undergoes a strong pressure treatment, its allowable stress can be increased by 20%.
- Carbon cable spring steel is divided into four groups based on its mechanical properties, with Group 1 having the highest tensile strength, Group II in second place, Group III having the lowest, and Group IV having the same tensile strength as Group II but better plasticity.
The Sb of carbon cable spring steel wire can be found in the table.
Strength of carbon spring steel wire
| Code | MP | |||
|---|---|---|---|---|
| Group I | Group II | Group III | ||
| Wire diameter d / Mn | 0.2 | 2700 | 2250 | 1750 |
| 0.3 | 2700 | 2250 | 1750 | |
| 0.5 | 2650 | 2200 | 1700 | |
| 0.8 | 2600 | 2150 | 1700 | |
| 1 | 2500 | 2050 | 1650 | |
| 1.5 | 2200 | 1850 | 1450 | |
| 2 | 2000 | 1800 | 1400 | |
| 2.5 | 1800 | 1650 | 1300 | |
| 3 | 1700 | 1650 | 1300 | |
| 3.6 | 1650 | 1550 | 1200 | |
| 4 | 1600 | 1500 | 1150 | |
| 4.5 | 1500 | 1400 | 1150 | |
| 5 | 1500 | 1400 | 1100 | |
| 5.6 | 1450 | 1350 | ||
| 6 | 1450 | 1350 | 1050 | |
| 7 | 1250 | 1000 | ||
| 8 | 1250 | 1000 | ||
4. Manufacture of spring
The process of producing a coil spring involves rolling, creating hooks or completing end face rings, heat treatment, and performance testing.
In large-scale production, the springs are rolled using a universal automatic coiling machine. For individual pieces or small batch production, they are crafted using a traditional lathe or by hand. When the diameter of the spring wire is 8mm or less, a cold coiling method is typically utilized.
Heat treatment is necessary before coiling, with low-temperature tempering required after coiling. When the diameter is greater than 8mm, a hot coiling method (with temperatures ranging from 800°C to 1000°C) should be employed. After hot coiling, the spring should be quenched and tempered at medium temperatures.
After the spring has been formed, a surface quality inspection should be performed to ensure it is smooth and free of defects such as scars, decarburization, and other imperfections. Springs that will be subjected to variable loads should also undergo surface treatment, such as shot peening, to improve their fatigue life.
5. End structure of spring
The effective number of turns N participating in the deformation of the compression spring is crucial in ensuring the spring works evenly and its center line is perpendicular to the end face.
To achieve this, there are 3/4 to 7/4 turns at both ends of the spring that play a tight supporting role, known as dead circles or supporting rings. These turns do not participate in the deformation during work.
The tension spring is equipped with a hook at its end for installation and loading, and there are four common types of end structures: semicircular shackle, circular shackle, adjustable hook, and rotatable hook.
Semicircular and circular shackles are easy to manufacture and widely used, but due to high bending stress at the transition of the hook, they are only suitable for springs with a spring wire diameter d ≤ 10mm. On the other hand, adjustable and rotatable hooks are under good stress conditions and can be turned to any position for easy installation.
6. Stress calculation of spring
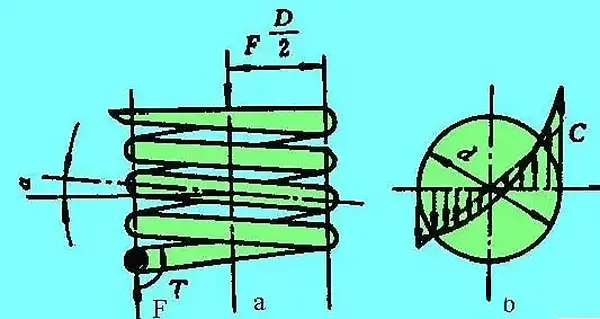
Stress analysis of compression spring
Fig. (a) shows the cylindrical helical compression spring, which bears the axial working load F.
The section method analysis reveals that the spring wire section is subjected to both a shear force F and a torque T, which is equal to F times D divided by 2. The torque results in a shear stress, which can be calculated as follows:
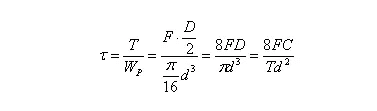
If we take into account the impact of shear stress generated by the shear force F and the spiral curvature of the spring wire, the maximum shear stress t can be found on the inner side of the spring, as depicted in figure (b). Its value and strength conditions are as follows:
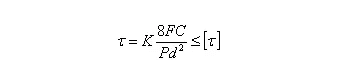
Where,
C – winding ratio,
C = D / D, which can be selected according to table 1
K — spring curvature coefficient,
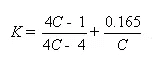
K can also be found directly from table 2.
It is known from the table that the greater C, the smaller the influence of K on T;
F — working load of spring, N;
D — pitch diameter of spring, mm;
D – material diameter mm.
Table 1 recommended values of winding ratio
| Steel wire dia. D | 0.2~0.6 | 0.5~1 | 1.1~2.2 | 2.5~6 | 7~16 | 18~50 |
| C=D/d | 7~14 | 5~12 | 5~10 | 4~9 | 4~8 | 4~6 |
Table 2 curvature coefficient K
| Winding ratio C | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 |
| K | 1.4 | 1.31 | 1.25 | 1.21 | 1.18 | 1.16 | 1.14 | 1.2 | 1.1 |
In equation 1, the formula for calculating the diameter of spring steel wire according to the strength condition can be obtained by replacing f with the maximum working load F2 of spring:
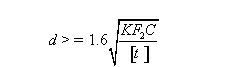
The method for calculating the strength of a tension spring is identical to that of a compression spring.
7. The spring is not in place and the failure reason
In practical work, it is common to encounter situations where the spring cannot push the moving object to the designated position, resulting in the calculated free length of the spring becoming shorter.
The cause of this issue is the lack of initial compression treatment, which involves compressing the spring to its compression height or tightening height using a significant amount of force (if necessary), and then releasing it so that it returns to its original free length.
The amount by which the spring has shortened is referred to as “initial compression shrinkage.”
Typically, after being subjected to compression 3-6 times, the length of the spring will no longer shorten and it will have “settled into its position.”
It is important to note that after undergoing initial compression, the spring is permanently deformed.
8. Spring precautions
In practical applications, a compression spring should be able to maintain its working length even if it is subjected to forces that exceed the elastic limit of its material.
As a result, the length of the finished spring should equal the calculated length of the spring plus the initial compression shrinkage. This will prevent the spring from not being in place and reduce the risk of dangerous stress when the spring coils are tightened together, leading to an abnormal spring deflection.
During the heat treatment of the finished spring, particularly the hardening and tempering process, it is crucial to place the workpiece horizontally (lying down) in the furnace to prevent the spring from becoming shorter due to its own weight, which could result in improper operation.
