Bükülme Ödeneği Hesaplayıcısı (Çevrimiçi ve Ücretsiz)

Bükülme Ödeneğini Anlama

Bükme payı, sac metal imalatında temel bir kavramdır ve bükülmüş metal parçalarda doğru boyutlara ulaşmak için gereklidir. Bükme işlemi sırasında malzemede meydana gelen uzamayı hesaba katarak parçanın nihai boyutlarının tasarım özelliklerine uygun olmasını sağlar.

Bükülme Ödeneğinin Tanımı

Bükme payı, bükmenin başlangıcından sonuna kadar tarafsız eksenin uzunluğunu ifade eder. Nötr eksen, bükme sırasında hiçbir sıkıştırma veya uzamaya maruz kalmayan malzeme içindeki hayali bir çizgidir. Bu hesaplama, büküldüğünde malzemenin deformasyonunu dikkate aldığından, bir sac metal parçanın düz desen düzenini belirlemek için çok önemlidir.

Sac Metal Tasarımındaki Önemi

Bükme payının doğru hesaplanması birkaç nedenden dolayı hayati önem taşır. İlk olarak, bükülen parçanın nihai boyutlarının tasarım özelliklerine uygun olmasını sağlar. Ayrıca, ihtiyaç duyulan malzeme miktarını doğru bir şekilde tahmin ederek malzeme israfını en aza indirmeye yardımcı olur. İsraftaki bu azalma, hata ve yeniden işleme riskini azaltarak üretim sürecinde maliyet tasarrufu sağlar.

Bükülme Payını Etkileyen Faktörler

Bükülme payını etkileyen çeşitli faktörler vardır. Malzeme kalınlığı (T) önemli bir rol oynar, çünkü daha kalın malzemeler daha ince malzemelere kıyasla farklı bükülme özelliklerine sahiptir. Tipik olarak tamamlayıcı açı olarak ölçülen bükülme açısı (θ), malzemenin ne kadar esneyeceğini etkiler. Malzemenin iç tarafındaki bükümün iç yarıçapı (r) da hesaplamayı etkiler. Son olarak, malzeme kalınlığı ile nötr eksen arasındaki oranı temsil eden malzemeye özgü bir sabit olan K faktörü (K) çok önemlidir.

Bükülme Ödeneği Formülü

Bükülme payı aşağıdaki formül kullanılarak hesaplanabilir:

Nerede?

• ( BA ) bükülme payıdır.
• ( θ ) derece cinsinden bükülme açısıdır.
• ( π/180 ) dereceleri radyana dönüştürmek için bir dönüştürme faktörüdür.
• ( r ) iç yarıçaptır.
• ( K ) K faktörüdür.
• ( T ) malzeme kalınlığıdır.

Pratik Örnek

Aşağıdaki özelliklere sahip bir sac metal parça düşünün:

• Bükülme açısı (( θ )) = 90°
• İç yarıçap (( r )) = 5 mm
• Malzeme kalınlığı (( T )) = 2 mm
• K-faktörü (( K )) = 0,33

Bükülme payı formülünü kullanarak:

Bu hesaplama, sac metal parçanın düz desenini doğru bir şekilde geliştirmek için gereken bükülme payını sağlar.

I. Bükülme Ödeneği Hesaplayıcısı

Yeni ürünler için pres freni Bükülme payını hesaplamanın inceliklerine aşina olmayan operatörler için bükülme payı hesaplayıcısı paha biçilmez bir araç olabilir. Bu hesap makinesi süreci basitleştirerek doğru sonuçlar alınmasını sağlar ve günlük işleri daha verimli hale getirir.

Çevrimiçi büküm payı hesaplayıcıları, kullanıcıların malzeme kalınlığı, büküm açısı, iç yarıçap ve K faktörü gibi parametreleri girmesine olanak tanıyarak süreci basitleştirir. Bu hesaplayıcılar daha sonra bükülme payını ve bazen de bükülme kesintisini hesaplayarak doğru sac metal imalatını sağlar. Üreticiler bu araçları kullanarak zamandan tasarruf edebilir ve hesaplamalarında hata riskini azaltabilirler.

Hesaplama için Gerekli Parametreler

Bükülme payı hesaplayıcısını etkin bir şekilde kullanmak için operatörlerin aşağıdaki parametreleri girmesi gerekir:

1. Malzeme Kalınlığı: Malzemenin kalınlığı bükülme yarıçapını ve toplam bükülme payını etkiler.
2. İç Yarıçap: Malzemenin iç yüzeyindeki bükümün yarıçapı.
3. K-Factor: Bükme sırasında nötr eksenin konumunu belirlemeye yardımcı olan bir oran.
4. Bükülme Açısı: Malzemenin büküldüğü açı.

İlgili hesap makinesi:

• K Faktörü Hesaplayıcı
• Y Faktörü Hesaplayıcı
• Viraj Kesintisi Hesaplayıcı

Daha fazla okuma:

• Eğilme Payı, Eğilme İndirimi ve K-Faktörü Nasıl Hesaplanır?

II. Nedir Bükülme Ödeneği?

Bükme payı, şekillendirmeden sonra istenen nihai boyutlara ulaşmak için sac metal bükülürken gereken ek malzeme uzunluğudur. Bükme işlemi sırasında malzemede meydana gelen gerilme ve sıkışmayı telafi eder Bükme payı çeşitli faktörlere bağlı olarak değişir:

1. Malzeme özellikleri: Farklı malzemeler, bükme sırasında malzemenin ne kadar gerildiğini veya sıkıştığını etkileyen farklı esneklik ve plastisiteye sahiptir.
2. Sac kalınlığı: Daha kalın saclar genellikle aynı malzemenin daha ince saclarına kıyasla daha büyük bir bükülme payı gerektirir.
3. Bükme yöntemi ve takımlar: Bükme işleminin türü (örn. havalı bükme, dipten bükme, coining) ve bükme kalıbının tasarımı bükme payını etkileyebilir.
4. İç bükülme yarıçapı: Daha dar bir iç bükülme yarıçapı tipik olarak daha büyük bir yarıçaptan daha küçük bir bükülme payı gerektirir.

Bükülme payı değerleri tipik olarak ampirik veriler, matematiksel hesaplamalar ve pratik deneyimin bir kombinasyonu ile belirlenir. Deneyimli sac metal tasarımcıları ve mühendisleri, yıllar boyunca tekrarlanan testler ve doğrulamalar sonucunda bükülme payı tabloları ve formülleri geliştirmiştir.

Tasarımcılar, uygun bükme payı formülünü kullanarak veya güvenilir bükme payı tablolarına başvurarak, istenen nihai bükme boyutlarını verecek bir sac metal parçanın düz kalıp boyutlarını doğru bir şekilde hesaplayabilir. Bu, doğru düz kalıplar oluşturmak ve bükülen parçanın amaçlandığı gibi oturmasını ve çalışmasını sağlamak için çok önemlidir.

III. Bükülme Ödeneği Formülü

Bükme payı ve bükme kesintisi hesaplamaları, sac metal hammaddelerinin düz formdaki uzunluğunu belirlemek için kullanılan temel yöntemlerdir ve bükülen parçanın istenen boyuta ulaşmasını sağlar. Bu hesaplamaların anlaşılması, sac metal imalatında hassasiyet için çok önemlidir.

Bükülme Ödeneği Hesaplama Yöntemi:

Büküm payı (BA), bükümde kullanılacak malzemeyi hesaba katmak için düz levhanın toplam uzunluğuna eklenen malzeme miktarıdır. 

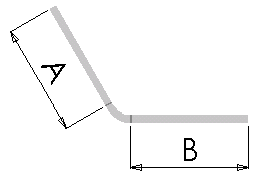
Bükülme payı değeri kullanıldığında toplam düzleştirme uzunluğunu belirlemek için aşağıdaki denklem kullanılır:

L_t = A + B + BA

Nerede?

• 𝐿_𝑡 toplam daire uzunluğudur.
• 𝐴 ve 𝐵, sac levhanın bükülmeden önceki iki düz bölümünün uzunluklarıdır (şekilde gösterildiği gibi).
• 𝐵𝐴 bükülme payı değeridir.

Viraj Kesintisi Hesaplama Yöntemi:

Büküm kesintisi (BD), bükümde kullanılacak malzemeyi hesaba katmak için düz levhanın toplam uzunluğundan çıkarılan malzeme miktarıdır. 

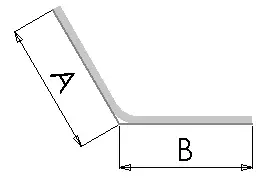
Bükme kesintisi değeri kullanılırken toplam düzleştirme uzunluğunu belirlemek için aşağıdaki denklem kullanılır:

L_t = A + B - BD

Nerede?

• 𝐿_𝑡 toplam daire uzunluğudur.
• 𝐴 ve 𝐵, sac levhanın bükülmeden önceki iki düz bölümünün uzunluklarıdır (şekilde gösterildiği gibi).
• 𝐵𝐷 bükülme kesintisi değeridir.

Diğer Hesaplama Yöntemleri

Bükme payı ve bükme kesintisi yöntemlerine ek olarak, sac metal hammaddelerin düz uzunluğunu belirlemek için başka teknikler de kullanılabilir. Bunlar şunları içerir:

• Bükme Payları Tablosu: Çeşitli malzemeler ve bükülme açıları için bükülme payı değerleri sağlayan önceden hesaplanmış bir çizelge.
• K-Faktörü: Malzemenin kalınlığına göre tarafsız eksenin konumunu temsil eden bir oran. Daha hassas eğilme hesaplamalarında kullanılır.
• Bükme Hesaplamaları: Bunlar, doğru sonuçlar elde etmek için malzeme özellikleri, bükülme yarıçapı ve kalınlık gibi daha karmaşık formüller ve değerlendirmeler içerir.

IV. Bükülme İzni Tablosu

1. SPCC için bükülme payı tablosu (yumuşak çelik)

2. SUS (paslanmaz çelik) için bükülme payı tablosu

3. SPHC (paslanmaz çelik) için bükülme payı tablosu

4. SECC için bükülme payı tablosu (galvanizli çelik sac)

5. Alüminyum levha için bükülme payı tablosu

V. K-Faktörünün Önemi

K-Faktörünün Tanımı ve Rolü

K-faktörü, sac metal imalatında önemli bir katsayıdır ve malzemenin kalınlığı içindeki nötr eksenin göreceli konumunu temsil eder. Nötr eksen, bükme işlemi sırasında hiçbir sıkıştırma veya gerilimin meydana gelmediği malzeme içindeki hayali düzlemdir. K-faktörü, iç yüzeyden nötr eksene olan mesafenin malzemenin toplam kalınlığına oranı olarak hesaplanır. K-faktörünün anlaşılması, bükülen parçaların nihai boyutlarının hassasiyetini sağlayan doğru bükme payı hesaplamaları için gereklidir.

Bükülme İzni Üzerindeki Etkisi

K faktörü, bükümü karşılamak için gereken ek malzeme uzunluğu olan büküm payını doğrudan etkiler. Tipik olarak bükülme açısı, iç yarıçap, malzeme kalınlığı ve K faktörünü içeren bükülme payı formülü şöyledir:

Burada ( BA ) bükme payı, ( θ ) radyan cinsinden bükme açısı, ( r ) iç yarıçap, ( K ) K faktörü ve ( T ) malzeme kalınlığıdır. Bu formül, hassas parça boyutları elde etmek ve malzeme israfını azaltmak için kritik olan bükme payının doğru bir şekilde hesaplanmasını sağlamada K faktörünün önemini vurgulamaktadır.

Malzeme ve Süreç Bağımlılığı

K-faktörü sabit bir değer değildir ve malzemenin özellikleri, bükme yöntemi, bükme yarıçapı ve bükme açısı dahil olmak üzere çeşitli faktörlere bağlı olarak değişir. Farklı malzemeler ve bükme koşulları, tipik olarak 0,3 ile 0,5 arasında değişen farklı K-faktörü değerleriyle sonuçlanacaktır. Örneğin, yüksek sünekliğe sahip bir malzeme, daha kırılgan bir malzemeye kıyasla farklı bir K faktörüne sahip olabilir, bu da bükme payını ve sonuç olarak parçanın nihai boyutlarını etkiler.

VI. Pratik Uygulama: Adım Adım Kılavuz

Adım 1: Gerekli Parametreleri Toplayın

Eğilme payını ve eğilme kesintisini doğru bir şekilde hesaplamak için aşağıdaki parametreleri toplayarak başlayın:

• Malzeme Kalınlığı (T): Sac metalin kalınlığını tipik olarak milimetre (mm) veya inç (inç) cinsinden ölçün.
• Bükülme Açısı (θ): Metal levhanın büküleceği açıyı belirleyin. Yaygın açılar arasında 90°, 120°, vb. bulunur.
• İç Yarıçap (IR): Malzemenin iç tarafındaki kıvrımın yarıçapını ölçün.
• K-Faktörü (K): K faktörü, malzemenin nötr ekseninin kalınlığına oranını temsil eder ve bir büküm için ne kadar malzeme gerektiğini belirlemek için gereklidir. Malzemenin özelliklerine ve kalınlığına bağlı olarak genellikle 0,3 ila 0,5 arasında değişir.

Adım 2: Bükülme Payını (BA) Hesaplayın

Büküm payı, bükümü karşılamak için gereken ek malzeme uzunluğunu hesaba katar. Bu değeri belirlemek için bükme payı formülünü kullanın:

Örnek Hesaplama:

• Malzeme Yumuşak Çelik
• Kalınlık (T): 0,125 inç
• İç Yarıçap (IR): 0,250 inç
• Bükülme Açısı (θ): 90 derece
• K-Faktörü (K): 0.42

1. Bükülme Açısını Radyana Dönüştürün:

2. Bükülme Ödeneği Formülünü uygulayın:

Adım 3: Dış Setback'i (OSSB) Hesaplayın

Ardından, viraj kesintisini hesaplamak için önemli olan dış setback'i belirleyin. OSSB için formül şöyledir:

Örnek Hesaplama:

• Bükülme Açısı (θ): 90 derece
• Malzeme Kalınlığı (T): 0,125 inç
• İç Yarıçap (IR): 0,250 inç

Bükülme Açısını Radyan'a Dönüştür:

Dış Setback Formülünü Uygulayın:

Adım 4: Bükülme Kesintisini (BD) Hesaplayın

Son olarak, sac metal imalatında doğru boyutlara ulaşmak için çok önemli olan büküm kesintisini belirlemek için dış gerileme ve büküm payını kullanın:

Örnek Hesaplama:

• Dış Setback (OSSB): 0,375 inç
• Bükülme Payı (BA): 0,475 inç

Viraj Kesintisi Formülünü Uygulayın:

Pratik Hususlar

Her bir parametrenin önemini anlamak, başarılı bükme işlemleri için hayati önem taşır. Örneğin K faktörü, büküm için ne kadar malzemeye ihtiyaç duyulacağını etkilerken büküm payı, malzemenin bükümden sonra doğru şekilde oturmasını sağlar. Ek olarak, metalin büküldükten sonra orijinal şekline hafifçe döndüğü ve malzemenin aşırı bükülmesini gerektirebilecek bir olgu olan geri yaylanmayı hesaba katmak önemlidir.

Bu adımları izleyerek ve her bir parametreyi dikkatlice değerlendirerek, hassas sac metal imalatı için gerekli büküm payını ve büküm kesintisini doğru bir şekilde hesaplayabilirsiniz.