Sac metal tasarımcılarının tasarımlarının doğruluğunu nasıl sağladıklarını hiç merak ettiniz mi? Bu blog yazısında, sac metal tasarımının büyüleyici dünyasına dalacağız ve iki temel kavramı keşfedeceğiz: bükme payı ve bükme kesintisi. Ayrıca K faktörünü ve hesaplamalardaki rolünü de tanıtacağız. Bu konuları çözerken ve sektör uzmanlarından değerli bilgiler sağlarken bize katılın.
Sac metal tasarımı alanında, bükme payı, bükme kesintisi ve K faktörü gibi terimler, üretim süreçlerinin doğruluğunu ve verimliliğini önemli ölçüde etkileyen çok önemli kavramlardır. Bu parametreler, bükülmüş sac metal parçaların nihai boyutlarının belirlenmesinde ve hassas imalatın sağlanmasında hayati bir rol oynar. Şimdi bu kavramları daha derinlemesine inceleyelim ve hesaplama yöntemlerini keşfedelim.
Sac metal imalatında yer alan mühendisler ve üreticiler, parçaların düz kalıp boyutlarını doğru bir şekilde hesaplamak için sofistike algoritmalar kullanır ve bükme ve şekillendirme işlemlerinden sonra hassas nihai geometriler sağlar.
Geleneksel "sıkıştırma yöntemi", malzeme özellikleri, bükme yarıçapı, bükme açısı, takım konfigürasyonları ve şekillendirme hızları gibi faktörleri içeren, yaygın olarak kullanılan ampirik bir yaklaşım olmaya devam etmektedir. Bu yöntem etkili olmakla birlikte, büyük ölçüde operatör deneyimine dayanır ve tutarsızlıklara maruz kalabilir.
Gelişmiş hesaplama araçlarının ortaya çıkmasıyla birlikte bilgisayar destekli tasarım (CAD) ve sonlu eleman analizi (FEA) sac metal tasarımının doğruluğu ve verimliliğinde devrim yaratmıştır. Bu teknolojiler, geri yaylanma, artık gerilmeler ve gerinim sertleşmesi gibi karmaşık olayları hesaba katarak şekillendirme işlemleri sırasında malzeme davranışının hassas bir şekilde simüle edilmesini sağlar.
Modern CAD sistemleri, teorik modelleri deneysel verilerle bütünleştiren gelişmiş bükülme telafisi algoritmaları kullanır. Bu algoritmalar tipik olarak iki temel yaklaşımdan birini kullanır:
SolidWorks, Autodesk Inventor ve Siemens NX gibi önde gelen CAD platformları, özelleştirilebilir büküm tabloları ve malzeme kütüphaneleri ile sağlam sac metal tasarım modülleri sunar. Bu sistemler, atölyeye özgü bükme verilerinin entegrasyonuna izin vererek dijital tasarımlar ve gerçek üretim süreçleri arasında uyum sağlar.
Ayrıca, makine öğrenimi ve yapay zeka gibi gelişmekte olan teknolojiler, tahminleri iyileştirmek ve benzersiz malzeme ve takım kombinasyonlarına uyum sağlamak için geçmiş üretim verilerinin geniş veri kümelerinden yararlanarak büküm hesaplamalarını optimize etmek için uygulanmaktadır.
Okuyucuların temel kavramları anlamalarını geliştirmek için sac metal tasarimi hesaplamasında aşağıdaki hususlar özetlenecek ve açıklanacaktır:
Daha net bir anlayış için bükülme payıBir sac metal parçadaki tek bir bükümü gösteren Şekil 1'e bakınız. Şekil 2, parçanın katlanmamış halini göstermektedir.
Şekil 1
Şekil 2
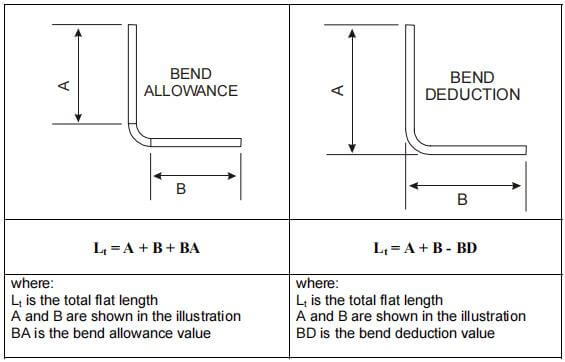
Bükme payı algoritması, bir sac metal parçanın katlanmamış uzunluğunu (LT), parça düzleştirildikten sonra her bir segmentin uzunluklarının toplamı artı düzleştirilmiş bükme alanının uzunluğu olarak tanımlar.
Bu bükülme payı (BA) düzleştirilmiş bükme alanının uzunluğunu temsil eder. Böylece, parçanın toplam uzunluğu denklem (1) olarak ifade edilebilir:
LT = D1 + D2 + BA (1)
Bükme alanı (resimde açık sarı olarak gösterilmiştir), bükme işlemi sırasında teorik olarak deformasyona uğrayan alandır.
Katlanmamış parçanın geometrisini belirlemek için aşağıdaki adımları izleyin:
Şekilde BA ile temsil edilen düzleştirilmiş bükülme alanının uzunluğunu belirleme görevi biraz daha zordur.
BA değeri, malzeme türü, malzeme kalınlığı gibi faktörlere bağlı olarak değişir, bükülme yarıçapı ve açının yanı sıra bükme işlemi, makine tipi ve makine hızı.
BA değeri, sac metal malzeme tedarikçileri, deneysel veriler, deneyim ve mühendislik kılavuzları dahil olmak üzere çeşitli kaynaklardan elde edilebilir.
SolidWorks'te BA değerleri doğrudan girilebilir veya değerleri hesaplamak için K faktörü (daha sonra ele alınacaktır) kullanılabilir.
Bu bükme masası yöntemi, farklı kalınlıklar, yarıçaplar ve açılara sahip farklı durumlar için farklı eğilme payları belirlemenin en doğru yoludur.
İlk bükme tablasını oluşturmak biraz zaman alabilir, ancak bir kez oluşturulduktan sonra, parçaları gelecekte yeniden kullanılabilir.
Parçadaki her bir büküm için aynı veya farklı bilgiler girilebilir.
1) Ortak Bükme için Standartlar
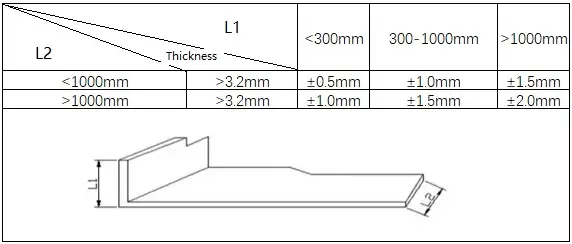
2) Z Bükme için Standartlar
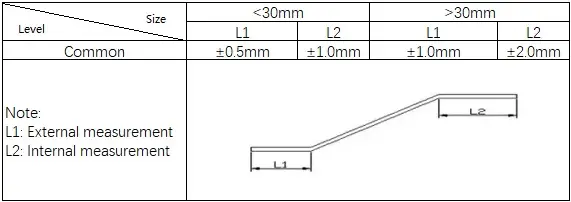
3) V Bükme için Standartlar
4) Standartlar için U Bükme
İlgili okuma: V ve U Şeklinde Bükme Kuvveti Hesaplayıcı
Bükme Kesintisi, bükme işlemindeki gerileme miktarını tanımlamak için kullanılan bir terimdir. sac metal bükme. Bu, süreci tanımlamak için başka bir basit algoritmadır.
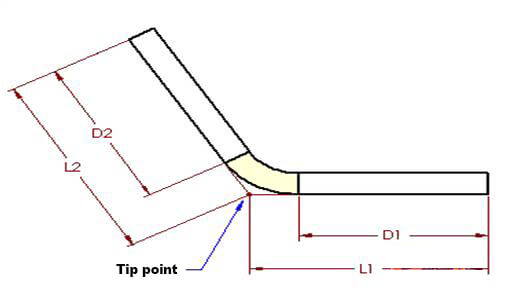
Şekil 1 ve 2 de bu kavram için geçerlidir. Eğilme kesintisi yöntemine göre, parçanın düzleştirilmiş uzunluğu (LT), "uç noktasına" (iki düz bölümün varsayımsal kesişme noktası) kadar uzanan iki düz bölümün uzunluklarının toplamından eğilme kesintisinin (BD) çıkarılmasına eşittir.
Böylece, parçanın toplam uzunluğu denklem (2)'de gösterildiği gibi ifade edilebilir:
LT = L1 + L2 - BD (2)
BD'nin değeri aşağıdaki gibi çeşitli kaynaklardan belirlenebilir veya elde edilebilir metal malzeme tedarikçiler, deneysel veriler, deneyimler, denklemler veya tablolar içeren mühendislik kılavuzları vb.
Şekil 3
Bükme Kesintisi yöntemine aşina olan kullanıcıların SolidWorks'te yaygın olarak kullanılan Bükme Ödeneği yöntemiyle olan ilişkiyi anlaması önemlidir.
İki değer arasındaki ilişki, parçaların bükülmesi ve açılmasına ilişkin iki geometri kullanılarak kolayca çıkarılabilir.
Denklem (1) ve (2)'yi karşılaştırarak şunu elde ederiz:
LT = D1 + D2 + BA (1) LT = L1 + L2 - BD (2)
Ve bu yüzden,
D1 + D2 + BA = L1 + L2 - BD (3)
Şekil 3'te, A açısı bükme açısıBu, bükme sırasında parça tarafından süpürülen açıyı ve ayrıca iki yarıda gösterilen bükme alanı tarafından oluşturulan yayın açısını tanımlar.
Dik üçgenlerin boyutlarını ve ilkelerini kullanarak aşağıdaki denklemleri türetebiliriz:
D1 = L1 - (R + T)TAN(A/2) (4) D2 = L2 - (R + T)TAN(A/2) (5)
Denklem (4) ve (5)'i denklem (3)'te yerine koyarak BA ve BD arasındaki ilişkiyi elde edebiliriz:
BA = 2(R + T)TAN(A/2) - BD (6)
Bükülme açısı 90 derece olduğunda, bu denklem basitleşir:
BA = 2(R + T) - BD (7)
Bu denklemler (6) ve (7), parametre olarak sadece malzeme kalınlığı, bükülme açısı/yarıçapı vb. kullanılarak bir algoritmadan diğerine dönüştürme için uygun bir yöntem sağlar.
SolidWorks kullanıcıları için bu denklemler, Bükme Kesintisini Bükme Payına dönüştürmek için doğrudan bir yöntem sağlar.
Bükme İzni değeri tüm parça veya her bir bükme için kullanılabilir veya bir bükme veri tablosuna dahil edilebilir.
K-faktörü, çeşitli geometrik senaryolarda sac metalin bükülmesini ve açılmasını açıklayan bağımsız bir değerdir.
Aynı zamanda farklı malzeme kalınlıkları, eğilme açıları ve yarıçaplar gibi çeşitli koşullar altında Eğilme Payını (BA) hesaplamak için kullanılan otonom bir değerdir.
Şekil 4 ve 5, K-faktörünün derinlemesine tanımını netleştirmeye yardımcı olmak için verilmiştir.
Şekil 4
Şekil 5
Sac metal parçanın kalınlığında nötr bir eksen olduğunu doğrulayabiliriz. Tabaka metal malzeme Eğilme bölgesindeki bu nötr eksen ne gerilir ne de sıkıştırılır, yani eğilme sırasında deforme olmayan tek alandır.
Şekil 4 ve 5 pembe ve mavi bölgeler arasındaki sınırı göstermektedir.
Bükme sırasında pembe bölge sıkışır ve mavi bölge uzar. Nötr sac metal katman deforme olmadan kalırsa, bükme bölgesindeki yayının uzunluğu, parça bükülse de düzleştirilse de aynı kalır.
Sonuç olarak, bükülme payı (BA), Şekil 4'te yeşil renkle gösterilen sac metal parçanın bükülme bölgesindeki nötr katmanın yay uzunluğuna eşit olmalıdır.
Sac metalin nötr tabakasının konumu, süneklik gibi belirli bir malzemenin özelliklerine bağlıdır.
Nötr sac metal katman ile yüzey arasındaki mesafenin "t" veya sac metal parçanın yüzeyinden kalınlık yönünde malzemenin içine doğru olan derinlik olduğu varsayılır.
Sonuç olarak, nötr tabakanın yayının yarıçapı (R + t) olarak ifade edilebilir. Bu ifade ve bükülme açısı kullanılarak nötr tabaka yayının uzunluğu (BA) hesaplanabilir.
BA = Pi(R+T)A/180
Sac metal nötr tabakanın tanımını basitleştirmek ve tüm malzemelere uygulanabilir hale getirmek için K-faktörü kavramı ortaya atılmıştır.
K-faktörünün tanımı şudur: sac metalin nötr tabakasının kalınlığının sac metal parça malzemesinin toplam kalınlığına oranıdır. Başka bir deyişle, K-faktörü şu şekilde tanımlanır:
K = t/T
Bu nedenle, K değeri her zaman 0 ila 1 aralığında olacaktır. Bir K faktörü 0,25 ise, nötr tabakanın sac metal malzemenin toplam kalınlığının 25%'sinde yer aldığını gösterir.
Aynı şekilde, 0,5 ise, nötr katmanın tüm kalınlığın 50%'sinde yer aldığını gösterir ve bu böyle devam eder.
Yukarıda belirtilen denklemler birleştirilerek aşağıdaki denklem (8) elde edilebilir:
BA = Pi(R+K*T)A/180 (8)
Bu nedenle, K değeri her zaman 0 ile 1 arasında olacaktır.
Bir K faktörü 0,25 ise, nötr tabakanın parça sac malzemesinin kalınlığının 25%'sinde bulunduğu anlamına gelir.
Benzer şekilde, 0,5 ise, nötr tabakanın tüm kalınlığın 50%'sinde yer aldığı anlamına gelir ve bu böyle devam eder.
K-faktörünün kökeni, sac metal malzeme tedarikçileri, test verileri, deneyim, kılavuzlar vb. gibi geleneksel kaynaklara kadar uzanabilir.
Ancak bazı durumlarda, sağlanan değer net bir K faktörü olarak ifade edilemeyebilir, ancak yine de aralarındaki ilişkiyi bulmak mümkündür.
Örneğin, bir kılavuz veya literatür nötr ekseni "sac metal yüzeyinden 0,445x malzeme kalınlığında konumlandırılmış" olarak tanımlıyorsa, bu 0,445'lik bir K faktörü olarak yorumlanabilir, yani k = 0,445.
Bu K değeri denklem (8)'de yerine konulduğunda aşağıdaki formül elde edilebilir.
BA = A (0,01745R + 0,00778T)
Denklem (8) başka bir yöntemle değiştirilirse, denklem (8)'deki sabit hesaplanır ve tüm değişkenler korunursa, aşağıdakiler elde edilebilir:
BA = A (0,01745 R + 0,01745 K*T)
İki denklemi karşılaştırarak, 0,01745 * k = 0,00778 olduğunu belirlemek kolaydır ve bu nedenle k 0,445 olarak hesaplanabilir.
SolidWorks sisteminin, bükülme açısı 90 derece olduğunda belirli malzemeler için bir bükülme payı algoritması da sağladığı keşfedilmiştir. Her malzeme için hesaplama formülü aşağıdaki gibidir:
Aslında, denklem (7) basitleştirilerek ve bükülme açısı 90 derece olarak ayarlanarak sabit hesaplanabilir ve denklem aşağıdaki gibi dönüştürülebilir:
BA = (1,57 * K * T) + (1,57 * R)
Bu nedenle, yukarıdaki hesaplama formülü karşılaştırılarak, yumuşak pirinç veya yumuşak bakır malzemeler için K değeri 1.57xk = 0.55 veya K = 0.35 olarak elde edilebilir.
Aynı yöntemi kullanarak, yukarıda listelenen çeşitli malzeme türleri için K-faktörü değerlerini hesaplamak kolaydır.
Daha önce tartışıldığı gibi, K-faktörü değerinin elde edilebileceği malzeme tedarikçileri, test verileri, deneyim ve kılavuzlar gibi çeşitli kaynaklar vardır.
K-faktörü yöntemini kullanarak doğru bir sac metal modeli oluşturmak için mühendislik gereksinimlerinizi karşılayan uygun K-faktörü kaynağını bulmak çok önemlidir. Bu, fiziksel parça sonuçlarının istenildiği kadar doğru olmasını sağlayacaktır.
Bazı durumlarda, özellikle de çok çeşitli bükülme senaryolarına uyum sağlanması gerektiğinde, tek bir K faktörü değeri kullanarak doğru sonuçlar elde etmek mümkün olmayabilir.
Bu gibi durumlarda, tüm parçanın tek bir bükümü için doğrudan bükme payı (BA) değerinin kullanılması veya tüm aralıktaki farklı A, R ve T değerlerine karşılık gelen farklı BA, bükme kesintisi (BD) veya K faktörü değerlerini tanımlamak için bir bükme tablosu kullanılması tavsiye edilir.
Ayrıca, SolidWorks tarafından sağlanan örnek bükülme tablosu gibi verileri oluşturmak için denklemler kullanılabilir. Gerekirse, bükme tablosundaki hücreler deneysel veya ampirik verilere dayalı olarak da değiştirilebilir.
SolidWorks'ün kurulum dizini, gerektiğinde düzenlenebilen ve özelleştirilebilen bükme payı tablolarını, bükme kesintisi tablolarını ve K faktörü tablolarını içerir.
Bu yazı, sac metal parçaların tasarım ve imalatında kullanılan yaygın hesaplama yöntemlerine ve bunların altında yatan ilkelere kapsamlı bir genel bakış sunmaktadır.
Eğilme paylarının, eğilme indirimlerinin ve K-faktörlerinin hesaplanmasını kapsar ve bu yöntemler arasındaki farkları ve birbirleriyle olan ilişkilerini açıklar.
Sektördeki mühendisler ve teknik profesyoneller için faydalı bir referans niteliğindedir.
Not:
MachineMFG'nin kurucusu olarak, kariyerimin on yıldan fazlasını metal işleme sektörüne adadım. Kapsamlı deneyimim, sac metal imalatı, talaşlı imalat, makine mühendisliği ve metaller için takım tezgahları alanlarında uzman olmamı sağladı. Bu konular hakkında sürekli düşünüyor, okuyor ve yazıyorum, sürekli olarak alanımın ön saflarında kalmaya çalışıyorum. Bilgi ve uzmanlığımın işiniz için bir değer olmasına izin verin.
TR 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO