Hiç sac metal parçaları doğru bir şekilde açmakta zorlandınız mı? Bu makale, sac metal açma hesaplamalarının arkasındaki sanat ve bilimi araştırıyor. Karmaşık geometrileri hassas bir şekilde açmak için deneyimli mühendisler tarafından kullanılan temel kavramları, formülleri ve teknikleri keşfedin. Bu ilkeleri kendi tasarımlarınıza nasıl uygulayacağınızı ve üretim sürecinizi nasıl kolaylaştıracağınızı öğrenin.
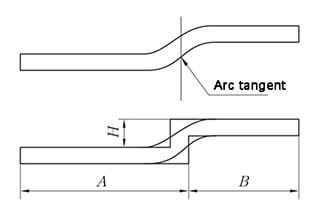
Sac metal imalat sürecinin ilk adımı, geometrilerin ve uyumlu gövdenin açılmasıdır. Numune açılımının doğruluğu ve kesinliği nihai parçanın kalitesini doğrudan etkiler.
Geçmişte, hesaplama araçlarının sınırlamaları nedeniyle, insanlar numuneyi 1:1 oranında bir düzlem üzerinde büyütmek ve gerekli plan çizgisinin gerçek uzunluğunu ölçmek için projeksiyon yöntemini kullanırlardı.
Ancak bu yöntem karmaşık ve verimsizdir ve mevcut üretim taleplerini karşılayamamaktadır.
Elektronik hesap makineleri ve bilgisayarların yaygın kullanımı gibi hesaplama araçlarındaki gelişmelerle birlikte, sac metal açılım artık hesaplama yöntemleri kullanılarak gerçekleştirilebilir.
Teknisyenler tarafından sac metal açma katsayısının hesaplama yöntemini standartlaştırmak, bükme işleminden sonra ürünlerin boyutsal sapmalarını en aza indirmek ve atölye personeli tarafından kendi kendini denetlemeyi ve kalite denetçileri tarafından yeniden denetlemeyi kolaylaştırmak için, açma katsayısı için birleşik bir standart ve temel vardır.
Sonuç olarak, sac metal açma katsayısı için hesaplama standardı giderek daha standart hale gelmiştir.
Nötr Katman Açma Yöntemi
Bükme işleminde, dış katman çekme gerilimine maruz kalırken, iç katman basınç gerilimine maruz kalır. Çekme ve basma gerilimi arasındaki geçiş katmanı nötr katman olarak adlandırılır. Bükme sırasında nötr tabakanın uzunluğu bükme öncesiyle aynı kalır ve bu da bükülen parçanın katlanmamış uzunluğunu belirlemek için bir ölçüt oluşturur.
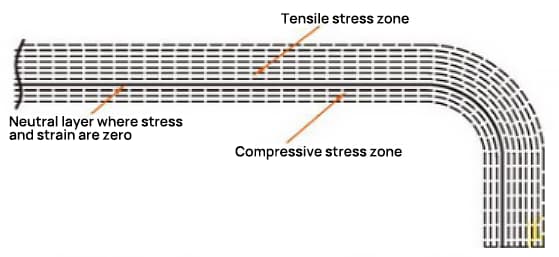
Nötr tabakanın konumu deformasyonun derecesine bağlıdır.
Nötr tabakanın konumu sadece bükülme yarıçapı, plaka kalınlığı, içe kayma katsayısı vb. ile değil, aynı zamanda işleme yöntemi, sac metal şekli ve boyutu gibi faktörlerle de ilgilidir.
Bu nedenle, nötr tabakanın konumu yalnızca yaklaşık olarak belirlenebilir ve pratik uygulamalarda, hesaplama için genellikle yaklaşık değerler kullanılır.
Nötr katmanın L uzunluk boyutu için hesaplama formülü şöyledir:
Bunların arasında,
Çeşitli kalınlıkların, açıların ve yarıçapların simülasyonlarını ve hesaplamalarını gerçekleştirmek için 3D yazılımı kullanarak ve sahadaki imalat uygulamalarıyla birlikte bir dizi K faktörü değeri derledik. Spesifik değerler için lütfen Tablo 1'e bakınız.
Tablo 1: Nötr Tabaka Katsayısı K-Değerleri
| r/t | ≤05 | 0.6 | 0.8 | 1 | 1.2 | 1.3 | 1.5 | 2 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | ≥8 |
| k | 026 | 0.28 | 0.30 | 0.32 | 0.33 | 0.34 | 0.36 | 0.38 | 0.39 | 0.4 | 0.42 | 0.44 | 0.46 | 0.5 |
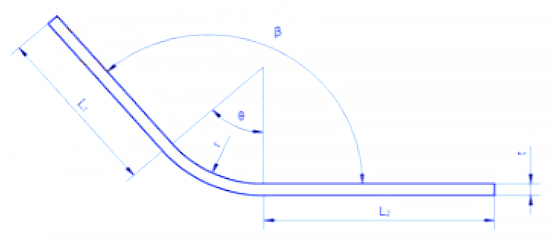
90° Bükümler için Hızlı Açılma Hesaplaması
90°'lik bir büküm için açılım diyagramı Şekil 9'da gösterilmektedir. Son yıllarda, açılma boyutlarını hesaplamak için sac metal modelleme için CATIA ve SOLIDWORKS gibi 3D yazılımları kullandık.
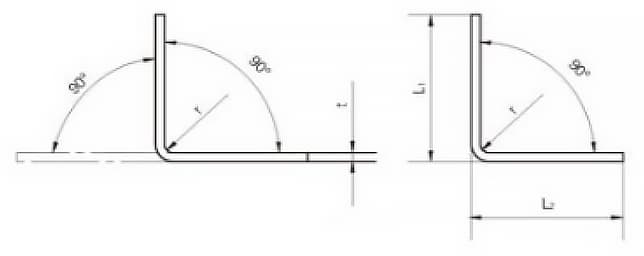
Tekrarlanan doğrulamalar sonucunda, yassı çelik ürünlerin soğuk bükme açısı 90° olduğunda, katlanmamış uzunluk L'nin hesaplanması için formülün şu şekilde olduğu görülmüştür:
L = L1 + L2 - A
Nerede?
Tablo 2 90° Bükme Parametreleri Tablosu
| Kalınlık t/mm | Yatak yarıçapı r/mm | |||||||||||
| 1 | 1.2 | 16 | 2 | 25 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | |
| Telafi değeri A mm | ||||||||||||
| 1 | -1.92 | -1.97 | -2.10 | -2.23 | -2.41 | -2.59 | -2.97 | -3.36 | -3.79 | -4.65 | -5.51 | -6.37 |
| 1.5 | -2.90 | -3.02 | -3.18 | -3.34 | -3.70 | -4.07 | -4.45 | -5.26 | -6.11 | -6.97 | ||
| 2 | -3.84 | -3.98 | -4.13 | -4.46 | -4.81 | -5.18 | -5.94 | -6.72 | -7.58 | |||
| 2.5 | -4.80 | -4.93 | -5.24 | -5.57 | -5.93 | -6.66 | -7.42 | -8.21 | ||||
| 3 | -5.76 | 6.04 | -6.35 | -6.69 | -7.40 | -8.14 | -8.91 | |||||
| 4 | -7.7 | -7.95 | -8.26 | -8.92 | -9.62 | -10.36 | ||||||
| 5 | -9.6 | -9.87 | -10.48 | -11.15 | -11.85 | |||||||
| 6 | -11.5 | -12.08 | -12.71 | -13.38 | ||||||||
| 8 | -15.4 | -15.9 | -16.51 | |||||||||
| 10 | -19.2 | -19.73 | ||||||||||
| 12 | 23.01 | |||||||||||
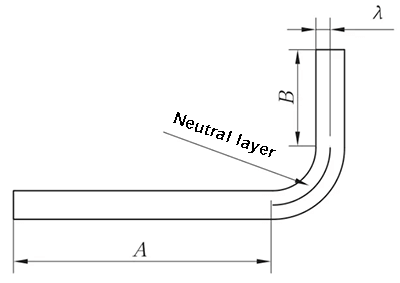
Ne zaman bükülme yarıçapı büyük ve bükülme açısı küçükse, deformasyon derecesi düşüktür ve nötr tabaka sac kalınlığının merkezine yakındır.
Bununla birlikte, bükülme yarıçapı (R) küçüldüğünde ve bükme açısı (θ) arttıkça, deformasyon derecesi de artar ve nötr tabaka bükme merkezinin iç tarafına doğru hareket eder. Nötr tabakadan tabakanın iç tarafına olan mesafe λ ile gösterilir ve malzeme kalınlığı T ile gösterilir.
Açılma uzunluğunu hesaplamak için temel formül:
Açılma uzunluğu = malzemenin iç boyutu + malzemenin iç boyutu + telafi miktarı.
Sac metal açılma uzunluğunu hesaplamak için aşağıdaki hesaplayıcıyı da kullanabilirsiniz:

Aşağıda çeşitli bükülme özelliklerinin açılma algoritmaları tek tek açıklanmaktadır.
R = 0mm, θ = 90° (Not: R ≤ 1.0mm olduğunda, R = 0mm olarak kabul edilir).
L = A + B + K
Gerçek üretimde, bükme üst kalıbı bir R açısı giyebilir veya 1 mm'den daha az bir R açısı olabilir veya alt kalıp'nin V yuvası diğer nedenlerin yanı sıra büyük olabilir ve bu da küçük bir eğilme katsayısına neden olur. Sonuç olarak, her bir malzeme plakası kalınlığının eğilme katsayısı, gerçek ampirik değerlere dayalı olarak Tablo 1'de sunulmuştur.
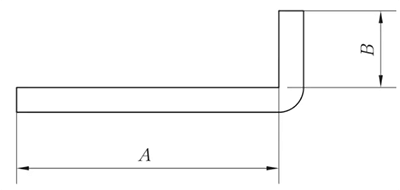
Şekil 1 Genel bükülmenin şematik diyagramı I
R ≠ 0mm ve θ = 90°
L = A + B + K (K nötr katmanın yay uzunluğudur)
Şekil 2 Genel bükme II'nin şematik diyagramı
R = 0mm, θ ≠ 90°
L = A + B + K'
Not: K, 90°'deki dengeleme miktarıdır.
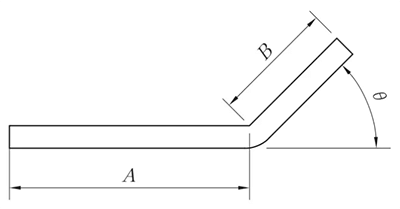
R ≠ 0mm, θ ≠ 90°
L = A + B + K
(K nötr katman yay uzunluğunu alır)
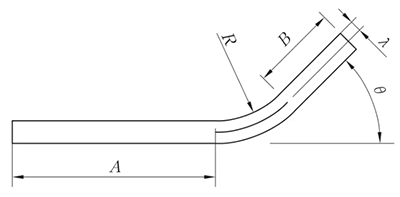
Şekil 4 Genel bükme IV bükme şeması
Açma Yöntemi, Paralel Düz Kenar Z-Katlama Yöntemine eşdeğerdir ve yükseklik ölçümü Şekil 6'da gösterilmiştir.
θ açısı 90°'lik bir açılma olarak kabul edilir.
0 < T ≤ 1,6 mm için λ 0,5T'ye eşittir.
T 1,6 mm'den büyük olduğunda, λ 0,4T'ye eşittir.
Z-Fold olarak da adlandırılır Ofset Bükmeşekillendirme açısına göre Düz Kenar Ofset Bükme ve Eğimli Kenar Ofset Bükme olarak ayrılır ve işleme yöntemi ofset yüksekliğine göre belirlenir.
Ofset yüksekliği, h, malzeme kalınlığının 3,5 katından az olduğunda, ofset kalıplar veya değiştirilebilir kalıplar şekillendirme için kullanılır.
Ofset yüksekliği malzeme kalınlığının 3,5 katını aşarsa, normal pozitif ve negatif şekillendirme kullanılır.
Eğimli kenarın uzunluğu malzeme kalınlığının 3,5 katından az olduğunda, şekillendirme için ofset kalıplar veya değiştirilebilir kalıplar kullanılır.
Eğimli kenarın uzunluğu malzeme kalınlığının 3,5 katını aşarsa, normal bir pozitif ve bir negatif katlama uygulanır.
(1) H < 3,5T olduğunda, ancak o zaman ofset bükme ile işlenebilir.
L = A + B + H
(H ≤ T ise, 0,2 mm telafi edin)
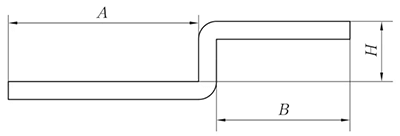
Şekil 5 Düz kenar ofsetinin şematik diyagramı
(2) Paralel olmayan düz kenar ofseti
Genişletme yöntemi paralel düz kenarlı Z-katlama yöntemiyle aynıdır ve yükseklik değeri Şekil 6'da gösterilmiştir.
θ açısı 90° açılmış olarak düşünülebilir.
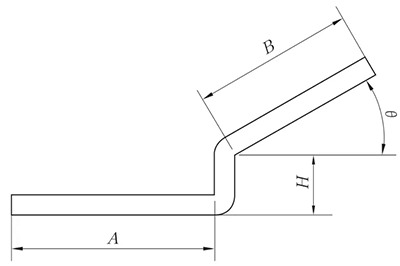
Şekil 6 Paralel olmayan düz kenar ofsetinin şematik diyagramı
(3) Düz kenar ofseti - geçiş segmenti iki yaya teğettir
Düz Kenar Ofseti iki dairesel yayın teğet noktasında açıldığında, alt tabakanın dış yüzeyindeki iki dairesel yayın teğet noktasında dikey bir çizgi oluşturulur. Daha sonra malzeme, işleme için Şekil 7'de gösterildiği gibi bir malzeme kalınlığı kadar içe kaydırılır ve Z-Katlama 1 (Düz Kenar Ofseti) yöntemi kullanılarak açılır.
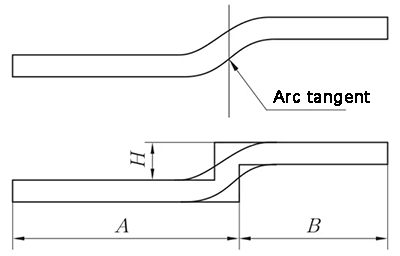
Şekil 7 Düz kenar ofset diyagramı - geçiş segmenti iki dairesel yaya teğettir
H < 2T olduğunda, açma algoritması ofset işlemine göre aşağıdaki gibidir.
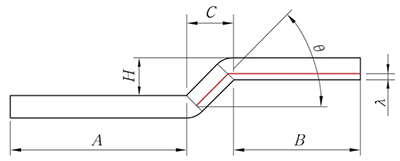
Şekil 8 Eğimli kenar ofsetinin şeması
L = A + B - K
(1) Düzleştirme yaparken, gerçek koşullara bağlı olarak bükme işleminden önce hattı bastırmayı düşünün.
Hat presleme konumu, bükülme deformasyon alanının merkezindedir.
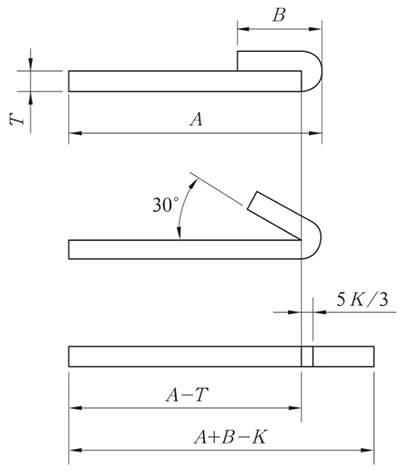
Şekil 9 Ters katlama ve düzleştirmenin şematik diyagramı
Ters Katlama ve Düzleştirme işlemleri genellikle iki adımda gerçekleştirilir: ilk olarak malzeme yerleştirme kalıbı kullanılarak 30° bükülür ve ardından düzleştirilir.
Bu nedenle, oluştururken bükme hattı genişletilmiş çizimde, Şekil 9'da gösterildiği gibi 150° bükmeye dayalı bükme hattının gösterilmesi önemlidir.
Tablo 1 Farklı kalınlıktaki plakaların farklı eğilme açıları altındaki eğilme katsayıları
| Açı | Kalınlık/mm | ||||
|---|---|---|---|---|---|
| 1 | 1.2 | 1.5 | 1.8 | 2.5 | |
| 45° | 5.3 | 6.3 | 7.8 | 9.5 | 13 |
| 50° | 4.5 | 5.4 | 6.8 | 8.1 | 11.25 |
| 55° | 4 | 4.7 | 5.8 | 7.05 | 9.75 |
| 60° | 3.4 | 4.1 | 5.1 | 6.15 | 8.5 |
| 65° | 3 | 3.6 | 4.5 | 5.4 | 7.5 |
| 70° | 2.65 | 3.2 | 4 | 4.75 | 6.6 |
| 75° | 2.35 | 2.8 | 3.5 | 4.25 | 5.9 |
| 80° | 2.1 | 2.5 | 3.1 | 3.75 | 5.25 |
| 85° | 1.9 | 2.25 | 2.8 | 3.35 | 4.65 |
| 90° | 1.7 | 2 | 2.5 | 3 | 4.15 |
| 95° | 1.5 | 1.8 | 2.2 | 2.7 | 3.75 |
| 100° | 1.35 | 1.6 | 2 | 2.4 | 3.35 |
| 105° | 1.2 | 1.4 | 1.75 | 2.15 | 3 |
| 110° | 1.1 | 1.3 | 1.6 | 2 | 2.65 |
| 115° | 1 | 1.25 | 1.4 | 1.7 | 2.35 |
| 120° | 0.85 | 1 | 1.25 | 1.5 | 2.1 |
| 125° | 0.75 | 0.9 | 1.1 | 1.35 | 1.85 |
| 130° | 0.65 | 0.8 | 1 | 1.18 | 1.65 |
| 135° | 0.55 | 0.7 | 0.85 | 1.05 | 1.45 |
| 140° | 0.5 | 0.6 | 0.75 | 0.9 | 1.25 |
| 145° | 0.43 | 0.5 | 0.65 | 0.77 | 1.05 |
| 150° | 0.35 | 0.43 | 0.55 | 0.65 | 0.9 |
| 155° | 0.3 | 0.35 | 0.45 | 0.53 | 0.75 |
| 160° | 0.23 | 0.27 | 0.35 | 0.4 | 0.6 |
| 165° | 0.17 | 0.2 | 0.25 | 0.3 | 0.45 |
N-katlı işleme yöntemi hem yeniden şekillendirme hem de düzleştirme içerir ve katlama algoritması şöyledir:
L = A + B + K
(K nötr katman yay uzunluğunu alır).
λ = 0,5T
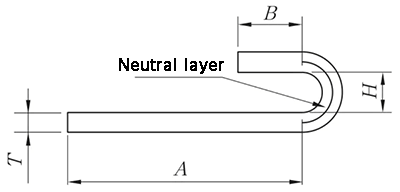
Şekil 10 N-kat diyagramı
(1) Ark genişlemesi doğrudan K'dır ve nötr katmanın ark uzunluğu alınır. λ= 0,5T
(2) Bir tarafta düz kenar ile genişletme.
L = A + K
(k nötr katmanın yay uzunluğudur)
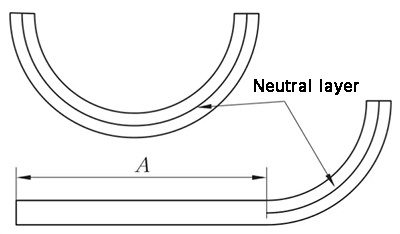
Şekil 11 Ark bükmenin şematik diyagramı
Gerçek üretimde, 3D yazılım aracılığıyla sac metalin katlanmamış uzunluğunun hassas kontrolü esas olarak aşağıdaki adımlar ve yöntemlerle sağlanabilir:
Doğru 3D tasarım yazılımını seçin: Öncelikle sac metal tasarımı için uygun bir 3D CAD yazılımı seçmeniz gerekir. SolidEdge, Creo, FreeCAD, UG, vb. sac metal tasarımı için kullanılabilecek yazılımlardır. Bu yazılımlar, tasarımcılara sac metal parçaların tasarımı ve açılma hesaplamalarında yardımcı olabilecek sac metal modülleri veya ilgili işlevler sağlar.
Sac levha modülünü veya yazılımdaki araçları kullanın: Çoğu 3D CAD yazılımı, sac metal tasarımı için ilgili araçlar ve işlevler sağlar. Örneğin Creo, büyük ark sac parçalarının modellenmesi ve açılma yöntemleri, bükülme kesintisi yöntemi vb. dahil olmak üzere sac metalin katlanmamış boyutlarını kontrol etmek için çeşitli yöntemler sunar. Açık kaynaklı bir 3D modelleme yazılımı olan FreeCAD de bir sac levha modülü sunmaktadır.
Uygulamaly unfolding hesaplama yöntemleri: Sac metal açıldıktan sonra uzunluğun doğruluğunu sağlamak için farklı açma hesaplama yöntemleri kullanılabilir. Yaygın yöntemler arasında bükülme telafisi yöntemi, bükülme çıkarma yöntemi ve K faktörü hesaplama yöntemi yer alır. Bu yöntemler, tasarımcıların katlanmamış durumdaki malzemenin gerçek uzunluğunu hesaplamasına yardımcı olabilir, böylece son bükme ve şekillendirmeden sonra parçaların beklenen boyutunu sağlar.
Kenar ve köşe kullanımına ve detay ayarına dikkat edin: Sac metal tasarım sürecinde, kenar ve köşe işleme detayları çok önemlidir. SW gibi bazı yazılımlar, açma doğruluğunu artırmaya yardımcı olan çeşitli kenar ve köşe işleme çözümleri ve bükme yöntemleri sağlar.
90 derecelik olmayan bükümler için yaygın büküm açıları 45 derece ve 135 dereceyi içerir ancak bunlarla sınırlı değildir. K faktörü için hesaplama yöntemi, malzeme kalınlığı ve bükülme yarıçapı arasındaki orana dayanır.
Spesifik olarak, K faktörü = δ / T, burada δ malzeme kalınlığını ve T bükülme yarıçapını temsil eder. Bu yöntem, 90 derece olmayan herhangi bir açının bükülme katsayısını hesaplamak için uygulanabilir.
Pratik uygulamalarda, farklı açılardaki bükümlerin çıkarım değerlerindeki olası farklılıklar ve büyük hatalar nedeniyle, büküm katsayısı olarak genellikle K faktörü kullanılır.
Ayrıca, farklı levha kalınlıklarının K faktörü değerini doğru bir şekilde yönlendirmek için ayarlamalar gereklidir. Bazı referanslar, herhangi bir bükülme yarıçapı için K faktörü değerinin, endüstriyel sac metal uygulamaları için etkili olduğu kanıtlanmış belirli enterpolasyon teknikleriyle hesaplanabileceğini önermektedir.
Eğimli pres-fren sacının genişletilmiş uzunluğu için hesaplama formülü şöyledir: [L = A + B + C + 0,2], burada (A), (B) ve (C) iç boyutları temsil eder ve 0,2 telafi değeri olarak kullanılır.
Sac metal genleşme hesaplamalarının genel ilke ve uygulamalarına dayanan bu telafi değeri, gerçek dünya operasyonları sırasında malzeme bükülmesi ve kalıp hassasiyeti hataları gibi faktörler nedeniyle gerçek ve teorik olarak hesaplanan uzunluklar arasındaki tutarsızlıkları açıklar.
Sac metal işlemede bu dengeleme değeri, nihai ürünün boyutsal doğruluğunu ve kalitesini sağlamaya yardımcı olur.
Sac metal parçalar elektromekanik, hafif sanayi ve otomotiv endüstrilerinde yaygın olarak kullanılmaktadır.
Sac metal parçaların katlanmamış formu, işlenmemiş parça boyutu için birincil belirleyici faktördür ve bu da işlenmemiş parçanın boyutunu ve şeklini etkiler.
Bununla birlikte, sac metal parçaların açılmasına yönelik geleneksel yöntemler, uzun döngüleri, düşük verimlilikleri ve düşük kaliteleri nedeniyle modern tasarım ihtiyaçlarını karşılamada giderek daha yetersiz hale gelmiştir.
Bu eksiklikleri gidermek için, gelişmiş CAD sistemlerinin kullanımı son yıllarda giderek yaygınlaşmaktadır.
Bu özel sac metal parça tasarım sistemleri sağlam işlevselliğe sahiptir ve sac metal parçaların ön tasarımı ve dağıtımı için gereken zaman ve çaba miktarını büyük ölçüde azaltabilir.