Metal bileşenlerinizi kesip açmadan tam olarak ne kadar gerilime dayanabileceklerini bildiğinizi hayal edin. X-ray kalıntı gerilme ölçümü, tahribatsız test yöntemlerini kullanarak bu bilgiyi sunar. Bu makalede, X ışını kırınım tekniklerinin iç gerilimleri nasıl doğru bir şekilde ölçerek ürün güvenilirliğini ve uzun ömürlülüğünü artırdığı anlatılmaktadır. Sin²ψ ve cosα teknikleri gibi farklı yöntemlerin hassas gerilme verileri sağlayarak metal işlerinizin en yüksek standartları karşılamasını nasıl sağladığını öğrenin. Bu gelişmiş ölçüm tekniklerinin prensiplerini, uygulamalarını ve endüstri mühendisliği için faydalarını anlamak için bu tekniklere dalın.
Artık gerilme, mühendislikte bu şekilde adlandırılan bir iç gerilme türüdür. Bir iş parçasındaki artık gerilimin dağılımı genellikle düzensizdir ve bu da statik mukavemetini, yorulma mukavemetini, şekil stabilitesini ve korozyon direncini önemli ölçüde etkileyebilir. Sonuç olarak, artık gerilimin ölçülmesi çok önemlidir.
Ölçüm için iki ana yöntem vardır artık gerilimTahribatlı testler ve tahribatsız testler. Tahribatlı test yöntemi, iş parçasının bir kısmının çıkarılmasını ve artık gerilim karşılık gelen gerilme ve yer değiştirmeye dayanır. Yaygın yıkıcı test yöntemleri şunları içerir delme yöntemi ve halka çekirdek yöntemi.
Tahribatsız test yöntemi, artık gerilmeyi hesaplamak için artık gerilme ile malzemede bir değişikliğe neden olabilecek fiziksel bir miktar (kristal düzlem aralığı, ultrasonik dalga yayılma hızı veya manyetik geçirgenlik gibi) arasında bir ilişki kurulmasını içerir. Tahribatsız test yöntemleri arasında X-ışını kırınımı, nötron kırınımı, manyetik ve ultrasonik yöntemler bulunur.
X-ışını kırınımı, olgun ilkeleri ve köklü yöntemlerinin yanı sıra laboratuvar cihazları, saha ölçümü için taşınabilir cihazlar ve özel durumlar için özel cihazlar da dahil olmak üzere giderek daha sofistike test ekipmanlarının mevcudiyeti nedeniyle artık gerilme ölçümü için en yaygın kullanılan yöntemdir.
Artık gerilmeyi ölçmek için X-ışını kırınımı yöntemi ilk olarak 1929 yılında Rus bilim adamı Akchenov tarafından önerilmiş ve makroskopik gerilmeyi kafes gerilmesi ile eşitlemiştir. Alman bilim adamı Macherauch 1961 yılında bu yöntemi daha da geliştirmiştir.2Akchenov'un fikrine dayanan ψ yöntemi, X-ışını kırınımı ile artık gerilme ölçümünü güvenilir ve yaygın olarak kullanılan bir teknoloji haline getirmiştir.
Geçtiğimiz 60 yıl içinde, X-ışını kırınımı birkaç farklı ölçüm yöntemine dönüşmüştür.2ψ yöntemi ve cosα yöntemi şu anda kullanılan iki ana yöntemdir.
Artık gerilimi ölçmeye yönelik X-ışını kırınımı teknolojisinde uzmanlaşmak için çeşitli yöntemlerini anlamak önemlidir.
(1) X-ışını kırınımı kalıntı gerilme ölçüm yöntemleri iki ana yaklaşım olarak kategorize edilebilir: sin2ψ yöntemi ve cosα yöntemi.
(2) Günah2ψ yöntemi, artık gerilme hesaplama yöntemine göre 2θ yöntemi, d-değeri yöntemi ve gerinim yöntemi olarak sınıflandırılabilir.
(3) ψ ve 2θ arasındaki geometrik ilişkiye dayanarak, sin2ψ yöntemi iki türe ayrılabilir: eş eğim yöntemi ve yuvarlanma yöntemi.
(4) Ölçüm yöntemi, X-ışını tüpü ve sayaç tüpünün tarama moduna göre sabit ψ0 yöntemi ve sabit ψ yöntemi olarak da farklılaştırılabilir.
(5) Rulo yöntemi içinde üç alt kategori vardır: standart rulo yöntemi, değiştirilmiş rulo yöntemi ve rulo sabitleme yöntemi ψ.
(6) Pozitif ve negatif ψ ölçüm yöntemi τφ kayma gerilmesini belirlemek için kullanılır.
(7) X-ışını kırınımı tipik olarak belirli bir noktadaki belirli bir yöndeki gerilimi ölçmek için kullanılır, ancak bir noktadaki asal gerilimi ölçmek için de yöntemler vardır.
(8) Salınım yöntemi birkaç alt kategoriye ayrılabilir: ψ0 salınım yöntemi, ψ salınım yöntemi, Debye halkası salınım yöntemi, φ açılı salınım yöntemi ve X/Y ileri geri öteleme yöntemi.
(9) Kırınım geometrisi açısından üç yaklaşım vardır: odaklama yöntemi, yarı odaklama yöntemi ve paralel ışın yöntemi.
Gerilme, gerinim tarafından belirlenir. Polikristal malzemeler söz konusu olduğunda, artık gerilme, ilgili bölgedeki kafes gerilmesinin istatistiksel sonucu ile tahmin edilir.
Böylece, artık gerilme X-ışını kırınımı tekniği ile kafes gerilmesi ölçülerek belirlenebilir.
Malzemenin artık gerilimi makro gerinimi yansıtır.
Makro gerinim, kafes gerinimine eşdeğerdir.
Kafes gerinimi, Bragg yasasına dayalı bir kırınım cihazı kullanılarak hesaplanabilen kristal düzlem aralığındaki göreceli değişimi temsil eder.
Bu, artık gerilmeyi ölçmek için X-ışını kırınım yöntemini özetlemektedir.
Bir polikristal belirli bir dalga boyuna (λ) sahip bir X-ışını demetine maruz bırakıldığında, Şekil 1'de gösterildiği gibi, yansıyan X-ışınının maksimum yoğunluğu (yani kırınım piki) belirli bir kırınım açısında (2θ) gözlemlenecektir. Bu olgu X-ışını kırınımı olarak bilinir.
X-ışını dalga boyu (λ), kristal düzlem aralığı (d) ve Bragg açısı (θ) arasındaki ilişki aşağıdaki denklem (1) ile açıklanmaktadır.

Artık gerilmenin X-ışını kırınım analizinde, uygun dalga boyunu (λ) belirlemek için X-ışını tüpü için uygun hedef malzeme seçilir. Kırınım açısı (2θ) daha sonra bir kırınım cihazı kullanılarak ölçülür. Ölçüme dayanarak, ilgili kristal düzleminin kristal düzlem aralığı (d) hesaplanabilir.

Şekil 1 X-ışını kırınım geometrisi
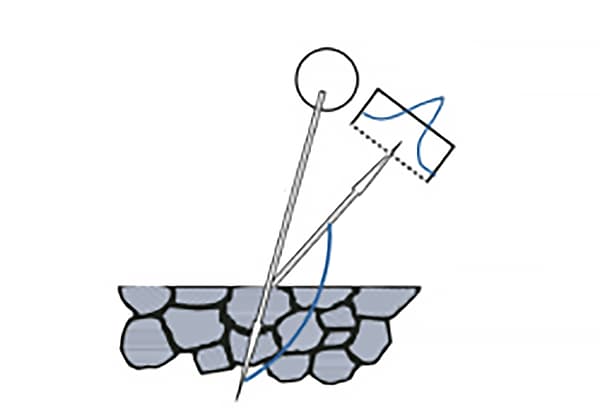
Optiğin yansıma yasasına göre, kırınıma dahil olan kristal düzlemin normali, Şekil 2'de gösterildiği gibi, gelen ve yansıyan ışınlar arasındaki açıortay üzerinde olmalıdır.
Kırınım kristali düzleminin normali ile numune yüzeyinin normali arasındaki açı, kırınım kristali düzleminin normalinin azimut açısı olarak bilinir ve genellikle ψ ile gösterilir.

Şekil 2 X-ışını Kırınımının Şematik Diyagramı Kristal Düzlemi Azimut ψ
Bragg yasası, belirli bir yönelimdeki (ψ) kristal düzlemlerin aralığının (dψ) belirlenmesini sağlar.
Gerilimsiz durumdaki kristal düzlemlerin aralığı (d0) biliniyorsa, belirlenen yönelimdeki kafes gerilmesi (εψ) hesaplanabilir.
S1, S2 ve S3 numune yüzeyinin eksenleridir ve S1 araştırmacı tarafından tanımlanır.
Şekil 3, X-ışını kırınımı yoluyla artık gerilimi ölçmek için kullanılan koordinat sistemini göstermektedir.

Şekil 3 X-ışını kırınımı stres ölçümü için koordinat sistemi
Genelleştirilmiş Hooke yasasına göre, bu kristal düzlemlerin gerilmeleri O noktasındaki gerilme tensöründen etkilenir ve φ ve ψ'nin sinüs ve kosinüsü, malzemenin Young modülü ve Poisson oranı ile yakından bağlantılıdır.
Dolayısıyla, O noktasındaki gerilme (σφ) de dahil olmak üzere üç boyutlu gerilimi belirlemek mümkündür.
OP yönündeki gerilme ifadesi elastisite teorisinden türetilebilir.
Çoğu malzeme ve bileşen için, X-ışınlarının nüfuz derinliği yalnızca birkaç mikron ila onlarca mikrondur, bu nedenle genellikle σ33=0.
Bu nedenle, OP yönündeki gerilme denklem (2) ile temsil edilir.


Günah2ψ-yöntemi formülü Bragg yasası ve elastik teoriye dayalı olarak türetilmiştir.
Elastisite teorisinde ele alınan nesnelerin homojen, sürekli ve izotropik ortamlar olduğu varsayılır.
Ancak, bu varsayım sadece polikristal için geçerlidir metal malzemeler tane boyutu inceyse ve doku mevcut değilse.
Şekil 4, ε'nin fonksiyonel ilişki eğrisini göstermektedirn ve günah2ψ izotropik malzemeler, gerilme gradyanı veya bileşim gradyanı olan malzemeler, kayma gerilmeli malzemeler ve dokulu anizotropik malzemeler için.

Şekil 4c)'de gösterildiği gibi, eğer kayma gerilmesi τ13≠ 0, τ23≠0 ve sin2ψ eğrisi ± ψ çatallanmasına sahiptir, σφ ve τφ ölçülen gerinim verileri kullanılarak elde edilebilir ε﹢ψ ve ε-ψ Formül (4) ve Formül (5)'te gösterildiği gibi bir dizi ± ψ açısı üzerinde.

Şunu belirtmek önemlidir ki, günah2Şekil 4c'de gösterilen ψ eğrisi) ±ψ çatallanmasına sahip olma olasılığı düşüktür.
Bunun nedeni, kırınım için kullanılan X-ışınının test edilen malzemeye sınırlı penetrasyon derinliğine sahip olmasıdır, genellikle sadece birkaç mikron ila onlarca mikron.
Sonuç olarak, malzeme yüzeyine dik gerilme bileşenleri sıfır olarak kabul edilebilir.
Sadece özel işleme koşulları altında (güçlü ve büyük kesme miktarlı taşlama gibi) asal gerilme düzlemi numune yüzeyinden saptığında τ13≠0 ve τ23≠0 meydana gelir.
ψ çatallanması yaygın bir durum değildir ve uydurma eğrisi genellikle elips özelliğinden yoksundur. Bu büyük ölçüde gonyometrenin ±ψ mekanizmasındaki sistematik hatadan kaynaklanmaktadır. Bu nedenle, elips uydurmanın önemini fazla vurgulamaya gerek yoktur.
Sonuç olarak, X-ışını kırınımı yoluyla kalıntı gerilimi belirlemenin pratik ve uygulanabilir süreci, birkaç ψ açısı (veya birkaç ±ψ açısı çifti) seçmeyi ve karşılık gelen kırınım açısını (2θφψ) ölçmeyi ve ardından hesaplamayı içerir.
Araştırmacılar, ψ düzlemi ile 2θ düzlemi arasındaki uzaysal geometrik ilişkiyi düzenlemek, kırınım eğrisini belirlemek ve hesaplamalar yapmak için çeşitli yöntemler geliştirmişlerdir.
Kırınım açısı 2θφψ X-ışını kırınım cihazı tarafından ölçülür ve karşılık gelen kristal düzlem aralığı dφψ Bragg yasasına göre, kafes gerilmesi εφψ Formül (6)'da gösterildiği gibi kristal düzlem aralığı ile ifade edilebilir.

Gerçek gerilme, gerçek gerilme yöntemi ifadesi olan gerilmeyi hesaplamak için doğrudan Denklem (3), Denklem (4) ve Denklem (5)'te yerine konur.
Gerçek gerinim yöntemi benimsenmiştir ve d0 ve θ0 gerekli değildir.
Çoğu durumda, gerçek gerinim yönteminin önemli avantajları vardır.
Eşitlik (7) ve Eşitlik (8)'de gösterildiği gibi, gerinimi hesaplamak için yaklaşık denklemler de kullanılabilir.

2θ yönteminin hesaplama formülü denklem (9)'da gösterilmektedir.

Burada, K gerilme sabitidir ve hesaplama formülü denklem (10)'da gösterilmiştir.

Burada: ν malzemenin Poisson oranıdır.
Bazı malzemeler için θ0 kimyasal bileşimle büyük ölçüde değişir ve gerilme sabiti kullanılırsa sonuçlarda büyük sapmalar olacaktır.
Gerçek gerilme yöntemi, Avrupa Birliği standardı EN 15305-2008 Tahribatsız muayene - X-ışını kırınımı ile kalıntı gerilme analizi için test yöntemi ve GB/T 7704-2017 Tahribatsız Muayene X-ışını Gerilme Ölçüm Yöntemi'ne dahil edilmiştir.
XL-640 ev tipi gerilim ölçer, gerçek gerilme yöntemini varsayılan gerilim hesaplama yöntemi olarak listeler ve hesaplama için 2θ yöntemi seçilebilir.
Eş düzlem yöntemi, Şekil 5'te gösterildiği gibi 2θ düzleminin ψ düzlemi (gerilme yönü düzlemi) ile çakıştığı bir ölçüm yöntemidir.

Şekil 5 Aynı Eğim Yönteminin Geometrik Diyagramı
Aynı eğim yöntemiyle, X ışını geliş açısı ψ0 baskındır, ψ açısı ise Eşitlik (11) ve Eşitlik (12)'de gösterildiği gibi hesaplanabilir.

Gerçek iş parçasının gerilim testinde, test noktası benzer bir sığ olukta yer aldığında, gonyometrenin test alanı sınırlıdır, bu nedenle aynı eğim yöntemi daha uygundur.
Rulo yöntemi, Şekil 6'da gösterildiği gibi 2θ düzlemi ile ψ düzleminin (gerilme yönü düzlemi) birbirine dik olduğu bir ölçüm yöntemidir.

Şekil 6 Yuvarlanma Yönteminin Geometrik Diyagramı
Roll yönteminin (χ yöntemi) temel özelliği, gelişmiş ölçüm doğruluğuna katkıda bulunan kırınım pikinin küçük absorpsiyon faktörüdür.
2θ ve ψ aralıkları gerektiğinde tamamen genişletilebilir. Bazı malzemeler için, düşük tepe konumlarına sahip (145°'nin altındaki tepe noktaları gibi) difraktif ışınlar stres ölçümü için kullanılabilir.
Ancak, bu yöntemin 2θ düzlemi ve ψ düzlemi birbirine diktir, üç boyutlu bir alan gerektirir ve dar alanların ölçümüne uygulanmasını zorlaştırır.
Yabancı bir şirketin stres aleti ürünü, Şekil 7'de gösterildiği gibi çift dedektörlü modifiye bir Roll yöntemi kullanmaktadır. Geometrik düzeni şekilde gösterilmiştir.

Şekil 7 Modifiye Rulo Yönteminin Geometrik Diyagramı
Ocak 1977 gibi erken bir tarihte, Çin Bilimler Akademisi Metal Enstitüsü'nden Li Jiabao, Eşitlik (13) ve Eşitlik (14)'te gösterildiği gibi bu test yöntemini ve hesaplama formülünü önermiştir.
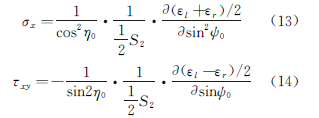
Rulo yöntemi iki kategoriye ayrılabilir: sabit ψ0 yöntemi ve sabit ψ yöntemi.
Sabit ψ yöntemi, daha doğru ilkeleri ve uygulamadaki etkili sonuçları nedeniyle sabit ψ0 yönteminden daha üstün kabul edilir.
Bu iki yöntemi birleştirerek, rulo sabit ψ yöntemi, absorpsiyon faktörü 1'e eşit olabilir.
Bu, kırınım pikinin arka dipte eğilmeyeceği, pik şeklinin simetrik kalacağı ve doku olmadığı sürece ψ açısı değişse bile pik şekli ve yoğunluğunun değişmeden kalacağı anlamına gelir.
Bu özellik ölçüm doğruluğunu büyük ölçüde artırarak rulo sabit ψ yöntemini ideal bir ölçüm tekniği haline getirir.
Salınım yöntemi, her bir ψ açısının (veya ψ0 açısının) bir merkez noktası olarak kullanılmasını ve X-ışını tüpü ile dedektörün belirli bir açıda (±Δψ veya ±Δψ0) sola ve sağa salınmasını içerir.
Bu yöntem, kırınıma katılan tane sayısını artırarak iri taneli malzemelerdeki gerilimi ölçmek için etkili bir yöntem haline getirir.
φ açılı salınım yöntemi ve X/Y ötelemeli salınım yöntemi gibi diğer salınım yöntemleri de kullanılabilir ve hatta test amacıyla farklı salınım yöntemleri birleştirilebilir.
2012 yılında, Japonya merkezli bir şirket olan PULSTEC, ilk kez iki boyutlu dedektör teknolojisini kullanan bir stres cihazını tanıttı.
Bu cihaz, X-ışını kırınım bilgilerini toplamak için tek bir olay modu ve iki boyutlu bir dedektör kullanarak çalışır ve test noktasında Debye halkası verilerini hızlı bir şekilde toplamasına olanak tanır.
Kristal yüzey normali ve numune yüzey normali tarafından oluşturulan ψ açısı Debye halkası üzerindeki her nokta için aynı düzlemde yer almadığından, sin2ψ yöntemi gerilimi hesaplamak için kullanılamaz. Bunun yerine, α açısı veya cosα yöntemi kullanılır (Şekil 8'de gösterildiği gibi).
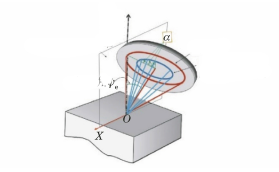
Şekil 8 cosα Yönteminin Geometrik Diyagramı
Bu test yöntemi, büyük çelik yapılarda yüzey gerilimini ölçmek için idealdir.
Bununla birlikte, kaba taneli malzemeleri veya dokulu malzemeleri test ederken sınırlamaları vardır.
cosα yöntemi, Denklem (15) ve (16)'da gösterildiği gibi esneklik ilkelerine dayanmaktadır.

Şekil 9, "tam iki konumlu dedektör" (45°'lik bir geliş açısıyla) kullanılarak elde edilebilecek maksimum ψ açısı aralığını göstermektedir.
α açısı, Debye halkası üzerindeki her bir noktanın merkez açısı olan Debye halka düzlemi üzerinde yer alır.

Şekil 9 Sin yönteminin veri noktalarının konumu2s eğrisinde ψ
X-ışını kırınımı yoluyla artık gerilimi ölçmek için kullanılan her iki yöntem de aynı mekanik prensibe dayanmaktadır.
Gerinim tensörü uzay açısında dönüştürülebilir ve cosα yönteminde kullanılan α açısı tamamen ψ açısına dönüştürülebilir.
Özünde, cosα yöntemi esasen sinα yönteminin bir yaklaşımıdır.2ψ yöntemi.
Tipik olarak, sıcak haddelenmiş çelik plakaların dokusuz olduğu kabul edilir. Bununla birlikte, bazı kısımları çelik levha çeşitli faktörlere bağlı olarak doku sergileyebilir.
Buna rağmen, birçok kullanıcı bu gibi durumlarda artık gerilimi ölçmek için X-ışını kırınımını kullanmayı tercih etmektedir.
Örneğin, dokulu sıcak haddelenmiş bir çelik levha seçilirse, test koşulları ve sonuçları Tablo 1 ve Tablo 2'de görülebilir. Her bir cihaz tarafından Z (0) noktasındaki artık gerilme ölçümü için test raporu Şekil 10-13'te gösterilmektedir.
Tablo 1 Sıcak Kalıntı Gerilme Ölçümü için Test Parametreleri Haddelenmiş Çelik Farklı Stres Enstrümanlarına Sahip Plaka
| Ekipman Türü | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| test yöntemi | cosα | günah2ψ | günah2ψ | günah2ψ |
| Gerilim/kV | 20 | 30 | 20 | 25 |
| Akım/mA | 1 | 25 | 1 | 6 |
| Aydınlatılmış nokta/mm | 1 | 1 | 1 | 1 |
| ψ Aralık/(°) | – | -35~35 | -40~40 | 0~45 |
| Gerilme hesaplama yöntemi | – | D değeri yöntemi | Gerinim yöntemi | Gerinim yöntemi |
| Tepe noktası belirleme yöntemi | – | KişiVII | Orta nokta | Çapraz korelasyon yöntemi |
| Artık gerilme/MPa | 78 | 213.6 | 144 | 113 |
Tablo 2 Sıcak Haddelenmiş Çelik Levhanın Farklı Gerilme Aletleri ile Ölçülen Kalıntı Gerilmesi
| Test noktası | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| Z(5) | 29,47 | 122 | 107 | 77 |
| Z(4) | 37,52 | 135 | 112 | 70 |
| Z(3) | 74,70 | 104 | 95 | 67 |
| Z(2) | 38,28 | 153 | 99 | 134 |
| Z(1) | 37,64 | 166 | 122 | 101 |
| Z(0) | 64,78 | 144 | 213 | 113 |
| Z(-1) | 72,71 | 138 | 97 | 139 |
| Z(-2) | 62,52 | 134 | 83 | 145 |
| Z(-3) | 75,70 | 120 | 93 | 153 |
| Z(-4) | 63,56 | 114 | 80 | 148 |
| Z(-5) | 79,27 | 94 | 93 | 152 |

Şekil 10 μ-X360S tipi gerilim ölçer ile ölçülen Z (0) noktasındaki Debye halkası

Şekil 11 2θ-sin2PROTO LXRD gerilim ölçer ile ölçülen Z (0) ψ eğrisi

Şekil 12 2θ-sin2X-RAYBOT Stres Ölçer ile Z (0) Ölçüm Noktasının ψ Eğrisi

Şekil 13 ε-sin2XL-640 gerilim ölçer ile ölçülen Z (0) ψ-eğrisi
c yöntemiyle ölçülen artık gerilme, s yöntemiyle ölçülenden daha küçüktür.
Z (0) test noktası için gerilim ölçer kullanılır. Sinüslerin eşit aralıklı olması ilkesine göre2ψ, 8 ψ açısı 0°~45° aralığında seçilir.
Sonuçlar Şekil 14-15'te gösterilmektedir. Görülebileceği gibi sin2Malzemenin ψ eğrisi, doku nedeniyle bir "şok" tipi sunar.
Günahın ordinatı2Şekil 13'teki ψ eğrisi ε gerinimidir. ordinatı 2θ olarak değiştirdikten sonra doğrusal uydurma gerçekleştirin. Sonuçlar Şekil 14'te gösterilmektedir.
Uyum çizgisinin eğimi M -0,355 ve artık gerilme σ 113MPa'dır.

Şekil 14 2θ-sin'in uydurma sonuçları2Z (0) noktasında XL-640 gerilim ölçer ile ölçülen ψ eğrisi
μ-X360S gerilim ölçer tarafından seçilen ψ aralığı, ekranlamanın ilk iki 2θ değerine eşdeğerdir ve ardından düz çizgi uydurma işlemi gerçekleştirilir. Sonuçlar Şekil 15'te gösterilmektedir.

Şekil 15 2θ-sin Uydurma Sonuçları2μ-X360S tipi Stres Aleti ile Ölçülen Z (0) ψ Eğrisi
Seçilen ψ aralığını test etmek için PROTO LXRD stres ölçer kullanın, Şekil 14'teki son üç 2θ değerini koruyun ve ardından doğrusal uydurma gerçekleştirin. Sonuçlar Şekil 16'da gösterilmektedir.

Şekil 16 2θ-sin'in uydurma sonuçları2Z (0) noktasında PROTO LXRD gerilim ölçer ile ölçülen ψ eğrisi
Şekil 12'den görülebileceği üzere maksimum sin2X-RAYBOT gerilim ölçer kullanılarak Z (0) noktasının ψ değeri 0,4 olarak belirlenmiştir.
Seçilen ψ aralığına göre, Şekil 14'teki son iki 2θ değerini koruyun ve ardından doğrusal uydurma gerçekleştirin. Sonuçlar Şekil 17'de gösterilmektedir.

Şekil 17 2θ-sin Uydurma Sonuçları2X-RAYBOT Stres Test Cihazı ile Ölçülen Z (0) ψ Eğrisi
Malzemenin dokusu nedeniyle, günahı2ψ eğrisi salınımlıdır.
Seçilen ψ açısı aralığı farklıdır, bu da uydurma çizgisinden elde edilen eğim ve artık gerilme değerlerinde farklılıklara neden olur.
Bilinmeyen dokulu ve iri taneli malzemeler için, önemli ölçüm hatalarına yol açabileceğinden, artık gerilme ölçümü için dar bir ψ aralığı ve az sayıda ψ istasyonu seçilmesi tavsiye edilmez.
Doğrusal montaj, dokulu sin içeren malzemeler için uygun olmayabilir2ψ eğrileri salınımlıdır.
Ölçüm işlemi sırasında, titreşimlerin ve ölçüm hatalarının neden olduğu dalgalanmaları azaltmak için genellikle doğrusal uydurma kullanılır.
Penetrasyon derinliğinden etkilenebileceğinden 45°'lik bir ψ açısına ulaşmak mümkün olmayabilir. Penetrasyon derinliğinin göz ardı edilebilmesi koşuluyla, daha büyük bir açının daha doğru sonuçlar üretmesi daha olasıdır.
Kaba taneli veya dokulu malzemeler için, doğrusal olmayan ε-sin etkilerini ortadan kaldırmak için ψ açısı aralığı mümkün olduğunca genişletilmelidir.2ψ dağılımı. Bu, her iki ±ψ açısının ölçülmesiyle elde edilebilir.
Uydurulan düz çizgilerin doğruluğu, regresyon uydurmak için en küçük kareler yöntemi kullanılarak ve hem ψ aralığı hem de ψ istasyonlarının sayısı artırılarak geliştirilebilir. Bu, daha güvenilir test değerleriyle sonuçlanacaktır.
Ölçüm doğruluğu, X-ışını pozlama alanını artırarak veya salınım yöntemiyle katılan kırınım tanelerinin sayısını artırarak da geliştirilebilir.
(1) Günah2ψ yöntemi, ψ aralığını artırarak ve daha fazla ψ istasyonu seçerek artık gerilmeyi gelişmiş doğrulukla belirlemek için kullanılabilir. Bununla birlikte, bu yöntem tek bir pozlama içerdiğinden sınırlamalara sahiptir ve bu da ψ aralığı yeterli değilse büyük ölçüm hatalarına neden olabilir.
(2) Sinüsün kullanıldığı ölçüm yöntemlerinde2ψ prensibine göre, yuvarlanma yöntemi eğme yönteminden daha üstündür. Ölçüm noktasındaki alan koşulları elverdiğinde yuvarlanma yönteminin kullanılması tavsiye edilir. Belirli bileşenlerin oluklarındaki artık gerilimi ölçmek için genellikle eş eğim yöntemi kullanılır.
(3) Gerçek gerinim yöntemi, artık gerilmenin hesaplanması için tercih edilen bir yöntemdir.
(4) sin2ψ yöntemi bu amaç için standart bir yöntem olarak kabul edilir. En doğru sonuçları elde etmek için, ψ açısı sin2ψ yöntemi kullanılarak ayarlanmalıdır.2ψ-değeri ikiye bölme yöntemi ile mümkün olduğunca çok sayıda ψ açısı ölçülmelidir.