Akma Dayanımını Anlamak: Kapsamlı Bir Kılavuz

Giriş

Akma dayanımının tanımı

Akma Dayanımı: Bu bir verim sınırıdır metal malzeme Akma olduğunda, yani hafif plastik deformasyona direnen gerilme.

İçin metal malzemeler belirgin bir akma olmaksızın, 0,2% artık deformasyon üreten gerilme değeri akma sınırı olarak belirtilir ve buna koşullu akma sınırı veya akma dayanımı denir.

Bu sınırdan daha büyük dış kuvvetler, bileşenin kalıcı olarak arızalanmasına neden olur ve geri yüklenemez. Örneğin, düşük karbonlu çeliğin akma sınırı 207 MPa'dır.

Bu sınırdan daha büyük dış kuvvetler uygulandığında, bileşen kalıcı deformasyona uğrayacaktır. Bundan daha az ise, bileşen orijinal formuna geri dönecektir.

Malzeme bilimi ve mühendisliğinde akma dayanımının önemi

Akma dayanımı, malzeme bilimi ve mühendisliğinde çok önemli bir rol oynar ve tasarım metodolojilerinde ve malzeme seçim süreçlerinde kritik bir parametre olarak hizmet eder. Geleneksel mukavemet tasarımı yaklaşımlarında, akma mukavemeti sünek malzemeler için bir ölçüttür ve izin verilen gerilme [σ] = σys/n olarak tanımlanır; burada σys akma mukavemeti ve n güvenlik faktörüdür. Bu güvenlik faktörü, özel uygulama gereksinimlerine ve çalışma koşullarına bağlı olarak tipik olarak 1,1 ila 2 veya daha yüksek bir değer arasında değişir.

Belirgin bir akma noktası olmayan gevrek malzemeler için nihai çekme dayanımı (σb) referans olarak kullanılır ve izin verilen gerilme [σ] = σb/n olarak hesaplanır. Bu durumlarda, malzemenin sınırlı plastik deformasyon kapasitesini ve ani kırılma modunu hesaba katmak için genellikle yaklaşık 6'lık daha muhafazakar bir güvenlik faktörü (n) kullanılır.

Geleneksel mukavemete dayalı tasarım metodolojisi genellikle akma mukavemetini en üst düzeye çıkarmaya odaklanmaya yol açsa da, bu yaklaşımın istenmeyen sonuçları olabileceğini kabul etmek çok önemlidir. Akma dayanımı arttıkça, kırılma tokluğunda genellikle buna karşılık gelen bir azalma olur ve bu da potansiyel olarak yıkıcı arıza riskini artırır. Bu ters ilişki, akma dayanımına tek başına odaklanmak yerine dengeli malzeme özelliği optimizasyonunun önemini vurgular.

Akma dayanımının önemi, gerilme hesaplamalarında doğrudan uygulanmasının ötesine geçer. Mühendislik uygulamalarında malzemelerin çeşitli mekanik davranışlarını ve işleme özelliklerini tahmin etmek için değerli bir gösterge olarak hizmet eder. Örneğin:

1. Stres korozyon direnci: Daha yüksek akma dayanımına sahip malzemeler, özellikle agresif ortamlarda, gerilme korozyonu çatlamasına karşı daha fazla duyarlılık gösterme eğilimindedir.
2. Hidrojen kırılganlığı: Daha yüksek mukavemetli malzemeler genellikle hidrojen kaynaklı çatlama ve gevrekleşme olaylarına daha yatkındır.
3. Şekillendirilebilirlik: Daha düşük akma dayanımlı malzemeler tipik olarak daha karmaşık şekillere ve daha düşük şekillendirme yüklerine izin veren üstün soğuk şekillendirme yetenekleri gösterir.
4. Kaynaklanabilirlik: Daha düşük akma dayanımına sahip malzemeler genellikle ısıdan etkilenen bölge çatlamasına ve artık gerilime bağlı distorsiyona karşı daha az duyarlılıkla gelişmiş kaynaklanabilirlik sergiler.
5. Yorulma performansı: Doğrudan ilişkili olmasa da akma dayanımı, özellikle yüksek çevrimli yorulma rejiminde yorulma davranışını etkileyebilir.
6. Aşınma direnci: Sertlik ve mikro yapı gibi diğer faktörler de önemli rol oynasa da, çoğu durumda daha yüksek akma dayanımı daha iyi aşınma direnci ile ilişkilidir.

Malzeme Gerilmesi ve Geriniminin Temelleri

Stres ve gerilme kavramları

Stres

Bir nesne dış etkenler (kuvvetler, nem, sıcaklık değişiklikleri, vb.) nedeniyle deforme olduğunda, nesnenin çeşitli parçaları arasında etkileşime giren iç kuvvetler vardır. Birim alan başına düşen iç kuvvete stres denir.

Kesite dik olanlara normal gerilim veya eksenel gerilim, kesite teğet olanlara ise kayma gerilimi veya kesme gerilimi denir.

Strain

Gerinim, diğer faktörlerin yanı sıra dış kuvvetlerin ve tekdüze olmayan sıcaklık alanlarının etkisi altında bir nesnenin göreceli deformasyonunu ifade eder.

Stres ve gerilme arasındaki ilişki

Hooke yasasına göre, belirli bir oransal sınır aralığı içinde, gerilme ve gerinim doğrusal bir oransal ilişkiye sahiptir.

Karşılık gelen maksimum gerilme oransal limit olarak adlandırılır.

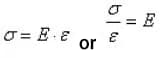
E ile gösterilen gerilimin gerilmeye oranına elastik modül veya Young modülü denir ve farklı malzemeler sabit bir Young modülüne sahiptir.

Stres doğrudan ölçülemese de, dış kuvvetlerin neden olduğu gerilme ölçülerek hesaplanabilir.

Ek Bilgi

Hooke yasası, katı malzemelerin gerilime maruz kaldıklarında gerilme ve gerinim (birim deformasyon) arasında doğrusal bir ilişki olduğunu belirten mekanik elastikiyet teorisinde temel bir yasadır.

Hooke yasasını karşılayan malzemeler doğrusal elastik veya Hookean malzemeler olarak adlandırılır.

Hooke yasasının ifadesi F=k-x veya ΔF=k-Δx şeklindedir; burada k bir sabittir, nesnenin sertlik (rijitlik) katsayısıdır.

Uluslararası Birimler Sisteminde F'nin birimi Newton, x'in birimi metredir ve bir deformasyon değişkenidir (elastik deformasyon) ve k'nın birimi Newton/metredir.

Sertlik katsayısı, yay bir birim uzunluk kadar gerildiğinde (veya kısaldığında) sayısal olarak yay kuvvetine eşittir.

Stres ve gerilme türleri

Stres türleri nelerdir?

Normal gerilme: Kesite dik olan gerilme bileşenine normal gerilme (veya eksenel gerilme) denir ve σ ile gösterilir.

Normal gerilme, parça içindeki bitişik kesitler arasındaki gerilme ve sıkışmayı temsil eder.

Normal gerilme: Bir noktadaki normal gerilme, kesit üzerinde bu yönde dağıtılan normal gerilme nedeniyle normal kuvvetin yönü boyunca uzamadır.

Kayma gerilmesi: Enine kesite teğet olan gerilme bileşenine kayma gerilmesi veya kayma kuvveti denir ve τ ile gösterilir. Kayma gerilmesi iki parça arasındaki kayma hareketini temsil eder.

Kayma gerilmesi: Bir noktadaki kayma gerilmesi, kesit üzerinde dağıtılan kayma gerilmesi nedeniyle iki dik yön arasındaki açıdaki değişimdir. Kayma deformasyonu olarak da bilinir.

Suş türleri nelerdir?

Temel olarak iki tür gerilme vardır: doğrusal gerilme ve açısal gerilme. Normal gerilme olarak da bilinen doğrusal gerilme, belirli bir yöndeki küçük bir doğru parçasının uzunluğundaki artışın (uzadığında pozitif) orijinal uzunluğuna oranıdır.

Kayma gerilmesi veya kayma deformasyonu olarak da bilinen açısal gerinim, kayma gerilmesi nedeniyle iki dik doğru parçası arasındaki açıdaki (azaldığında pozitif) değişimdir. Radyan cinsinden ifade edilir.

Akma Dayanımının Belirlenmesi

Gerilme-gerinim eğrisi

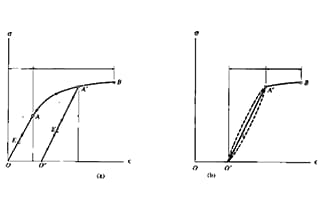
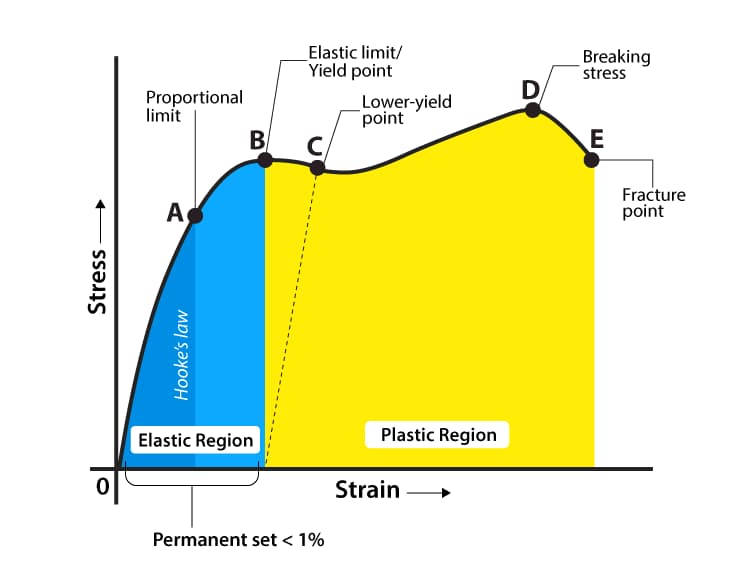
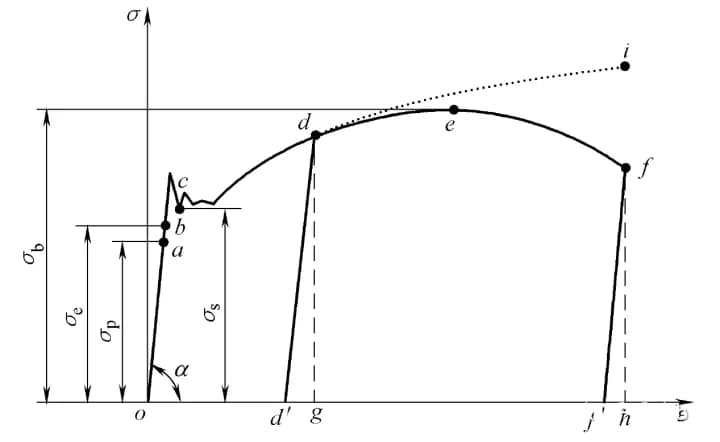
Gerilme-şekil değiştirme (σ-ε) eğrisi diyagramı Şekil 3'te gösterilmiştir.

Eksenel yük F yerine nominal gerilme σ = F / A0 alınır ve uzama Δl yerine mühendislik gerinimi ε = Δl / l0 alınır.

Gerilme-şekil değiştirme eğrisinin hala dört aşaması vardır. Her bir karakteristik noktanın anlamları şunlardır:

Sahne o'dan a'ya:

Gerilmenin (veya sıkıştırmanın) ilk aşamasında, gerilme σ ve şekil değiştirme ε a noktasına kadar doğrusal olarak ilişkilidir.

Bu noktada, a noktasına karşılık gelen gerilme değeri oransal limit olarak adlandırılır ve σp ile temsil edilir.

Gerilme ve gerinimin orantılı olduğu maksimum sınırdır.

σ≤σp olduğunda, Hooke yasası olarak da bilinen σ =Eε vardır, bu da gerilme ve gerinimin orantılı olduğunu gösterir.

Bu nedenle, E =σ / ε = tanα, burada E elastik modül veya Young modülü olarak bilinir ve birimleri σ ile aynıdır. Gerilme b noktasına ulaşmak için oransal sınırı aştığında, σ-ε ilişkisi düz bir çizgiden sapar.

Bu noktada gerilme sıfıra indirilirse, gerinim de ortadan kalkacaktır (gerilme b noktasını aştığında, gerinimin bir kısmı boşaltma sonrasında ortadan kaldırılamaz).

b noktasında tanımlanan gerilme, elastik limit σe olarak adlandırılır. σe, malzemenin sadece elastik deformasyonu için nihai limit değeridir.

Aşama B'den C'ye:

Gerilme elastik sınırı aştıktan sonra, gerilmenin çok az arttığı veya hiç artmadığı ve gerinimin hızla arttığı bir fenomen meydana gelir.

Bu olaya akma adı verilir. Akmanın başladığı nokta, akma dayanımı olarak da bilinen akma sınırı σs'ye karşılık gelir.

Akma aşamasında, gerilme değişmezken gerinim artmaya devam eder, malzeme deformasyona direnme yeteneğini kaybetmiş gibi görünür ve önemli plastik deformasyona neden olur (bu noktada yük boşaltılırsa, gerinim tamamen kaybolmaz ve artık deformasyon olur).

Bu nedenle, σs malzeme mukavemetini ölçmek için önemli bir indekstir.

Düşük karbonlu çelik bir numune yüzey parlatma ile akıtıldığında, yüzeyde kayma çizgileri olarak bilinen iç kristal kafesin göreceli kayması nedeniyle eksene 45 ° açıda çizgiler olacaktır.

C'den E'ye kadar:

Akma aşamasını geçtikten sonra, numune deforme olmaya devam edecekse, daha fazla yüklenmesi gerekir, malzeme güçlenmiş gibi görünür ve c-e aşaması güçlenme aşamasıdır.

Gerinim güçlendirme aşamasındaki en yüksek nokta (e noktası) mukavemet sınırı σb'ye karşılık gelir. Malzemenin dayanabileceği maksimum gerilimi temsil eder.

E'den F'ye kadar:

E noktasını geçtikten sonra, yani gerilme mukavemet sınırına ulaştıktan sonra, numune boyun verme olarak bilinen lokal olarak şiddetli bir büzülmeye maruz kalır.

Daha sonra, numunenin içinde çatlaklar meydana gelir, nominal gerilme σ azalır ve numune f noktasında kırılır.

Akma dayanımı (σs) ve çekme dayanımı (σb), akma dayanımının önemli göstergeleridir. malzeme dayanımı iyi plastikliğe sahip (düşük karbonlu çelik gibi).

Nominal gerilmenin kullanıldığına ve uzama deformasyonuna eşlik eden kesit alanındaki azalmanın dikkate alınmadığına dikkat edilmelidir.

Çekme dayanımı (σb) sadece malzemenin dayanabileceği nominal maksimum gerilimdir, malzemenin içindeki gerçek maksimum gerilim değildir.

Kırılma anında numunenin gerçek alanı ölçmek için kullanılırsa, gerçek maksimum gerilme, şekildeki d-i doğru parçası üzerindeki i noktasına karşılık gelen gerilme değeridir.

Mühendislik uygulamalarında, basitlik, pratiklik ve güvenlik adına, çekme mukavemeti (σb) hala malzemenin dayanabileceği maksimum gerilimi temsil etmek için kullanılmaktadır.

Ancak, malzemelerin doğrusal olmayan mekanik davranışlarını bilgisayar ile simüle ederken, gerçek gerilme-gerinim eğrisi kullanılmalıdır.

Akma dayanımını belirleme yöntemleri

Önemli akma fenomeni olmayan metaller için, öngörülen orantısız uzama veya artık gerilme gerilmesi altındaki çekme mukavemetleri ölçülebilir.

Önemli akma fenomenine sahip metaller için akma dayanımı, üst akma dayanımı ve alt akma dayanımı ölçülebilir.

Üst ve alt akma dayanımını ölçmek için iki yöntem vardır: grafik yöntemi ve işaretçi yöntemi.

Grafiksel Yöntem

Deney sırasında otomatik bir kayıt cihazı kullanılarak bir kuvvet-çene yer değiştirme grafiği çizilir.

Kuvvet ekseninin her milimetrenin temsil ettiği gerilime oranı 10 N/mm'den az olmalıdır²ve eğri en azından verim aşamasının sonuna kadar çizilmelidir.

Eğri üzerinde, akma sırasındaki sabit kuvvet Fe, akma aşamasında kuvvetteki ilk düşüşten önceki maksimum kuvvet Feh veya ilk anlık etkiden önceki minimum kuvvet FeL belirlenir.

Akma dayanımı, üst akma dayanımı ve alt akma dayanımı aşağıdaki formüller kullanılarak hesaplanabilir:

Akma dayanımı hesaplama formülü: Re = Fe/So; Fe akma sırasındaki sabit kuvvettir.

Üst akma dayanımı hesaplama formülü: Reh = Feh/So; Feh, akma aşaması sırasında kuvvetteki ilk düşüşten önceki maksimum kuvvettir.

Alt akma dayanımı hesaplama formülü: ReL = FeL/So; FeL ilk anlık etkiden önceki minimum kuvvettir.

Pointer Yöntemi

Deney sırasında, kuvvet ölçerin ibresi sabit kuvvette veya ilk geri dönüşten önceki maksimum kuvvette veya ilk anlık etkiden önceki minimum kuvvette dönmeyi bıraktığında, bunlar sırasıyla akma dayanımı, üst akma dayanımı ve alt akma dayanımına karşılık gelir.

Akma dayanımını etkileyen faktörler

Akma dayanımını etkileyen iç faktörler şunlardır: bağlanma, mikroyapı, yapı ve atomik yapı.

Verim karşılaştırması metallerin mukavemeti seramik ve polimerler ile bağlanma etkisinin temel olduğunu göstermektedir.

Mikroyapının etkisi açısından, metal malzemelerin akma dayanımını etkileyen dört güçlendirme mekanizması vardır:

(1) katı çözelti güçlendirmesi;

(2) gerinim sertleşmesi;

(3) çökelmenin güçlendirilmesi ve dağılımın güçlendirilmesi;

(4) tane sınırı ve alt tane güçlendirmesi. Çökelme ile güçlendirme ve ince taneli güçlendirme, endüstriyel alaşımların akma dayanımını artırmak için en yaygın kullanılan yöntemlerdir.

Bu güçlendirme mekanizmalarından ilk üçü malzemenin mukavemetini artırırken plastisiteyi de azaltır.

Sadece tane boyutunun ve alt tanelerin rafine edilmesi malzemenin mukavemetini ve plastisitesini artırabilir.

Akma dayanımını etkileyen dış faktörler şunlardır: sıcaklık, gerilme hızı ve gerilme durumu.

Sıcaklık düştükçe ve gerilme oranı arttıkça malzemenin akma dayanımı artar, özellikle gövde merkezli kübik metaller sıcaklığa ve gerilme oranına özellikle duyarlıdır, bu da çeliğin düşük sıcaklıkta gevrek kırılmasına yol açar.

 Gerilme durumunun etkisi de önemlidir. Akma dayanımı bir malzemenin doğal performansını yansıtmasına rağmen, akma dayanımı değeri gerilme durumuna bağlı olarak da farklıdır.

Bir malzemenin akma dayanımı genellikle tek eksenli gerilim altındaki akma dayanımı olarak adlandırılır.

Yaygın Malzemeler ve Akma Dayanımları

Akma Dayanımı için Test Yöntemleri

Akma dayanımı testi, malzeme dayanım özelliklerinin önemli bir göstergesi ve malzeme performansının kritik bir göstergesidir.

Genellikle malzeme yüzey mukavemetini ve plastik performansını değerlendirmek için kullanılır.

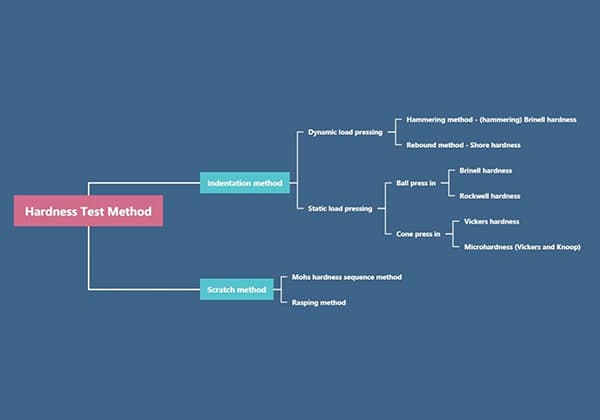
Akma dayanımı test yöntemleri genellikle iki türe ayrılır: mekanik ve mekanik olmayan.

Mekanik Akma Dayanımı Testi: 

Bu yöntem genellikle üç nokta eğme, çekme test makinesi yöntemi ve sıkıştırma yöntemini içerir. Numune iki destek arasına yerleştirilir ve akma dayanımını belirlemek için mekanik bir cihaz kullanılarak sabit bir kuvvet uygulanır.

Mekanik Olmayan Akma Dayanımı Testi:

Bu yöntem genellikle çekme, sıkıştırma ve burulma yöntemlerini içerir. Numune test cihazına monte edilir ve akma dayanımını belirlemek için bir kol veya bilgisayar kontrolü kullanılarak sabit bir kuvvet uygulanır.

Akma dayanımı testinin doğruluğunu ve hassasiyetini artırmak için, genellikle gerekli koşullar altında birden fazla test yapmak ve ortalama değeri almak gerekir.

Tüm deneylerde, numunenin işlenmesi standartlaştırılmış ve eksiksiz olmalı ve numune uygulanan kuvvet altında sabit tutulmalıdır. Elde edilen nihai akma dayanımı, malzemenin uygulanan yük altında bükülebileceği maksimum dayanımdır.

Sonuç

Bu makaleyi inceleyerek akma dayanımının ne olduğunu, gerilme ve şekil değiştirmenin temellerini, akma dayanımını belirleme yöntemlerini, akma dayanımını etkileyen faktörleri ve akma dayanımı uygulamalarını öğrendik.

Bu bilgilerin herkese yardımcı olacağını umuyoruz.

Herhangi bir sorunuz varsa, lütfen yorumlar bölümünde bize bildirmekten çekinmeyin.