Have you ever wondered how to accurately calculate the weight of wire mesh? In this blog post, we’ll explore various methods and factors to consider when determining wire mesh weight. Our resident mechanical engineering expert will guide you through the process, providing insights and practical examples. By the end of this article, you’ll have a clear understanding of how to estimate wire mesh weight for your specific needs.
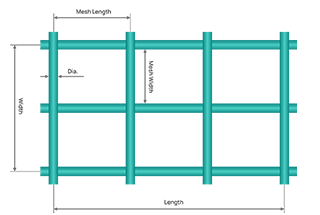
Wire mesh weight calculation is crucial in various applications, from construction to industrial manufacturing. Knowing how to accurately calculate the weight of wire mesh ensures that projects are carried out efficiently, safely, and within budget. The weight of wire mesh can be influenced by several factors, including the type of material, wire diameter, mesh count, and overall dimensions.

Wire Diameter: The thickness of the wire used in the mesh is a primary factor. It is measured in millimeters (mm) or inches. Thicker wires will result in a heavier mesh. For example, a wire diameter of 2 mm will produce a heavier mesh than a wire diameter of 1 mm, assuming all other factors are constant. This is because the volume of the wire increases with the square of the diameter, leading to a significant impact on weight.
Mesh Number: This refers to the number of openings per linear inch of the mesh. A higher mesh number means more wires and consequently more weight per unit area. For instance, a mesh with 10 openings per inch (10 mesh) will be lighter than a mesh with 20 openings per inch (20 mesh) if the wire diameter remains the same. This is due to the increased density of wires in the higher mesh number.
Mesh Opening/Aperture: The size of the openings between the wires, measured from center-to-center for mesh and inside-to-inside for openings, also affects the weight. Smaller apertures result in a denser, heavier mesh. For example, a mesh with an aperture of 1 mm will be heavier than one with a 5 mm aperture, assuming the wire diameter and mesh number are the same.
Material Type: Different materials have different densities, which directly affect the weight. Common materials include stainless steel, mild steel, aluminum, brass, and copper. For example, stainless steel has a density of approximately 7.93 g/cm³, while aluminum has a density of around 2.70 g/cm³. This means that for the same volume, stainless steel will be significantly heavier than aluminum.
Dimensions: The width and length of the wire mesh roll or panel also impact the total weight. These are typically measured in meters or feet. For example, a wire mesh panel measuring 10 meters by 1 meter will weigh more than a panel measuring 5 meters by 1 meter if all other factors are identical.
Just input the width, length, mesh width, mesh length, dia of the wire mesh in the calculator below, then you will get the result of wire mesh weight in both kg and lbs.
Calculating the weight of wire mesh is essential. It ensures precise planning in various industrial and construction projects. The weight calculation depends on wire diameter, mesh count, material density, and dimensions.
The weight calculation method for wire mesh can be determined in various ways, depending on the material, structure of the wire mesh, and specific parameters needed for calculation. We can summarize several different calculation methods and factors to consider.
Firstly, a basic weight calculation method involves estimating by dividing the product of wire diameter, mesh count, mesh length, and mesh width by 2. This method is applicable for general wire mesh weight calculations, where the unit of wire diameter is millimeters (mm), and the units for mesh length and width are meters (m).
Additionally, for specific types of wire mesh, such as galvanized wire mesh, more detailed calculation methods can be employed. For instance, the weight of galvanized wire mesh can be calculated by measuring the length of wire per square meter (in meters) and the weight of wire per meter (in kilograms). This method provides a straightforward way to estimate the weight of the wire mesh.
Another method is to calculate the weight through the cross-sectional area and length of the wire, as well as the density of the material. This can be achieved through the formula “Weight(kg) = Cross-sectional Area(mm2) × Length(m) × Density(g/cm3) × 1/1000″. This method is suitable for situations where precise calculation of wire mesh weight is required, particularly when considering the density of different materials.
The following simplified formula can be used to calculate the weight of steel wire mesh.
Weight (kg) = total length of raw materials * wire diameter² * coefficient (0.00617)
Stainless Steel Wire Mesh
Stainless steel is commonly used for its corrosion resistance and strength. For stainless steel wire mesh:
Mild Steel Wire Mesh
Mild steel is known for its durability and affordability. The calculation for mild steel wire mesh is similar to stainless steel but uses a different density factor:
Aluminum Wire Mesh
Aluminum is valued for its lightweight properties and resistance to corrosion. For aluminum wire mesh:
Brass and Copper Wire Mesh
Brass and copper are used for their excellent electrical conductivity and aesthetic appeal. For these materials:
For brass:
For copper:
To illustrate, let’s calculate the weight of a stainless steel wire mesh with the following specifications:
Using the general formula:
For stainless steel:
For the total weight:
By understanding these factors and applying the appropriate formulas, accurate weight calculations for wire mesh can be achieved, ensuring precise planning and execution in various projects.
The following table lists the theoretical weight of steel wire mesh in kg/m². If your steel size is not in the table below, you can use our steel weight calculator to calculate online.
(1) Longitudinal reinforcing bar weight chart
| Grade | Longitudinal reinforcing bar | Theoretical weight | ||
| Dia. | Distance | Area per linear meter | ||
| (mm) | (mm) | (mm²/m) | (kg/m²) | |
| A18 | 18 | 200 | 1273 | 14.43 |
| A16 | 16 | 200 | 1006 | 12.34 |
| A14 | 14 | 200 | 770 | 10.49 |
| A12 | 12 | 200 | 566 | 8.88 |
| A11 | 11 | 200 | 475 | 7.46 |
| A10 | 10 | 200 | 393 | 6.16 |
| A9 | 9 | 200 | 318 | 4.99 |
| A8 | 8 | 200 | 252 | 3.95 |
| A7 | 7 | 200 | 193 | 3.02 |
| A6 | 6 | 200 | 142 | 2.22 |
| A5 | 5 | 200 | 98 | 1.54 |
| B18 | 18 | 100 | 2545 | 24.42 |
| B16 | 16 | 100 | 2011 | 18.89 |
| B14 | 14 | 100 | 1539 | 15.19 |
| B12 | 12 | 100 | 1131 | 10.9 |
| B11 | 11 | 100 | 950 | 9.43 |
| B10 | 10 | 100 | 785 | 8.14 |
| B9 | 9 | 100 | 635 | 6.97 |
| B8 | 8 | 100 | 503 | 5.93 |
| B7 | 7 | 100 | 385 | 4.53 |
| B6 | 6 | 100 | 283 | 3.73 |
| B5 | 5 | 100 | 196 | 3.05 |
| C18 | 18 | 150 | 1697 | 17.77 |
| C16 | 16 | 150 | 1341 | 14.98 |
| C14 | 14 | 150 | 1027 | 12.51 |
| C12 | 12 | 150 | 754 | 10.36 |
| C11 | 11 | 150 | 634 | 8.7 |
| C10 | 10 | 150 | 523 | 7.19 |
| C9 | 9 | 150 | 423 | 5.82 |
| C8 | 8 | 150 | 335 | 4.61 |
| C7 | 7 | 150 | 257 | 3.53 |
| C6 | 6 | 150 | 189 | 2.6 |
| C5 | 5 | 150 | 131 | 1.8 |
| D18 | 18 | 100 | 1545 | 28.86 |
| D16 | 16 | 100 | 2011 | 24.68 |
| D14 | 14 | 100 | 1539 | 20.98 |
| D12 | 12 | 100 | 1131 | 17.75 |
| D11 | 11 | 100 | 950 | 14.92 |
| D10 | 10 | 100 | 785 | 12.33 |
| D9 | 9 | 100 | 635 | 9.98 |
| D8 | 8 | 100 | 503 | 7.9 |
| D7 | 7 | 100 | 385 | 6.04 |
| D6 | 6 | 100 | 283 | 4.44 |
| D5 | 5 | 100 | 196 | 3.08 |
| E18 | 18 | 150 | 1697 | 19.25 |
| E16 | 16 | 150 | 1341 | 16.46 |
| E14 | 14 | 150 | 1027 | 13.99 |
| E12 | 12 | 150 | 754 | 11.84 |
| E11 | 11 | 150 | 634 | 9.95 |
| E10 | 10 | 150 | 523 | 8.22 |
| E9 | 9 | 150 | 423 | 6.66 |
| E8 | 8 | 150 | 335 | 5.26 |
| E7 | 7 | 150 | 257 | 4.03 |
| E6 | 6 | 150 | 189 | 2.96 |
| E5 | 5 | 150 | 131 | 2.05 |
| F18 | 18 | 100 | 2545 | 25.9 |
| F16 | 16 | 100 | 2011 | 21.7 |
| F14 | 14 | 100 | 1539 | 18 |
| F12 | 12 | 100 | 1131 | 14.8 |
| F11 | 11 | 100 | 950 | 12.43 |
| F10 | 10 | 100 | 785 | 10.28 |
| F9 | 9 | 100 | 635 | 8.32 |
| F8 | 8 | 100 | 503 | 6.58 |
| F7 | 7 | 100 | 385 | 5.03 |
| F6 | 6 | 100 | 283 | 3.7 |
| F5 | 5 | 100 | 196 | 2.57 |
(2) Transverse reinforcing bar weight chart
| Grade | Transverse reinforcing bar | Theoretical weight | ||
| Dia. | Distance | Area per linear meter | ||
| (mm) | (mm) | (mm²/m) | (kg/m²) | |
| A18 | 12 | 200 | 566 | 14.43 |
| A16 | 12 | 200 | 566 | 12.34 |
| A14 | 12 | 200 | 566 | 10.49 |
| A12 | 12 | 200 | 566 | 8.88 |
| A11 | 11 | 200 | 475 | 7.46 |
| A10 | 10 | 200 | 393 | 6.16 |
| A9 | 9 | 200 | 318 | 4.99 |
| A8 | 8 | 200 | 252 | 3.95 |
| A7 | 7 | 200 | 193 | 3.02 |
| A6 | 6 | 200 | 142 | 2.22 |
| A5 | 5 | 200 | 98 | 1.54 |
| B18 | 12 | 200 | 566 | 24.42 |
| B16 | 10 | 200 | 393 | 18.89 |
| B14 | 10 | 200 | 393 | 15.19 |
| B12 | 8 | 200 | 252 | 10.9 |
| B11 | 8 | 200 | 252 | 9.43 |
| B10 | 8 | 200 | 252 | 8.14 |
| B9 | 8 | 200 | 252 | 6.97 |
| B8 | 8 | 200 | 252 | 5.93 |
| B7 | 7 | 200 | 193 | 4.53 |
| B6 | 7 | 200 | 193 | 3.73 |
| B5 | 7 | 200 | 193 | 3.05 |
| C18 | 12 | 200 | 566 | 17.77 |
| C16 | 12 | 200 | 566 | 14.98 |
| C14 | 12 | 200 | 566 | 12.51 |
| C12 | 12 | 200 | 566 | 10.36 |
| C11 | 11 | 200 | 475 | 8.7 |
| C10 | 10 | 200 | 393 | 7.19 |
| C9 | 9 | 200 | 318 | 5.82 |
| C8 | 8 | 200 | 252 | 4.61 |
| C7 | 7 | 200 | 193 | 3.53 |
| C6 | 6 | 200 | 142 | 2.6 |
| C5 | 5 | 200 | 98 | 1.8 |
| D18 | 12 | 100 | 1131 | 28.86 |
| D16 | 12 | 100 | 1131 | 24.68 |
| D14 | 12 | 100 | 1131 | 20.98 |
| D12 | 12 | 100 | 1131 | 17.75 |
| D11 | 11 | 100 | 950 | 14.92 |
| D10 | 10 | 100 | 785 | 12.33 |
| D9 | 9 | 100 | 635 | 9.98 |
| D8 | 8 | 100 | 503 | 7.9 |
| D7 | 7 | 100 | 385 | 6.04 |
| D6 | 6 | 100 | 283 | 4.44 |
| D5 | 5 | 100 | 196 | 3.08 |
| E18 | 12 | 150 | 754 | 19.25 |
| E16 | 12 | 150 | 754 | 16.46 |
| E14 | 12 | 150 | 754 | 13.99 |
| E12 | 12 | 150 | 754 | 11.84 |
| E11 | 11 | 150 | 634 | 9.95 |
| E10 | 10 | 150 | 523 | 8.22 |
| E9 | 9 | 150 | 423 | 6.66 |
| E8 | 8 | 150 | 335 | 5.26 |
| E7 | 7 | 150 | 257 | 4.03 |
| E6 | 6 | 150 | 189 | 2.96 |
| E5 | 5 | 150 | 131 | 2.05 |
| F18 | 12 | 150 | 754 | 25.9 |
| F16 | 12 | 150 | 754 | 21.7 |
| F14 | 12 | 150 | 754 | 18 |
| F12 | 12 | 150 | 754 | 14.8 |
| F11 | 11 | 150 | 634 | 12.43 |
| F10 | 10 | 150 | 523 | 10.28 |
| F9 | 9 | 150 | 423 | 8.32 |
| F8 | 8 | 150 | 335 | 6.58 |
| F7 | 7 | 150 | 257 | 5.03 |
| F6 | 6 | 150 | 189 | 3.7 |
| F5 | 5 | 150 | 131 | 2.57 |
Accurate wire mesh weight calculations are essential for various applications, from construction to manufacturing. Understanding the factors that influence these calculations ensures precision and reliability, which are crucial for effective planning and cost estimation.
Wire diameter, measured in millimeters (mm), significantly impacts the weight of wire mesh. The weight increases with the square of the wire diameter. For example, if a wire with a diameter of 2 mm weighs 1 kg per meter, a wire with a diameter of 4 mm will weigh 4 kg per meter, assuming other factors remain constant. This exponential relationship underscores the importance of precise wire diameter measurements.
Mesh count refers to the number of openings per inch in the wire mesh. A higher mesh count means more wires within a given area, increasing the overall weight. For instance, a 20 mesh (20 openings per inch) wire mesh will weigh more than a 10 mesh (10 openings per inch) wire mesh with the same wire diameter. Mesh count directly influences the density and weight of the mesh.
The dimensions of the wire mesh roll, including length and width, significantly impact the total weight. These dimensions are usually measured in meters or feet. For example, a wire mesh roll measuring 10 meters in length and 1 meter in width will weigh more than a roll measuring 5 meters by 1 meter, assuming the same wire diameter and mesh count. Accurate measurements of roll dimensions are essential for calculating the total weight.
Manufacturing tolerances can introduce variations in wire diameter, mesh count, and roll dimensions. These variations can affect weight calculations, leading to discrepancies between calculated and actual weights. Account for potential manufacturing variations and tolerances to ensure accuracy.
Different materials have distinct densities, directly affecting the weight of the wire mesh. Common materials include stainless steel, mild steel, aluminum, brass, and copper, each with its specific density. For example, stainless steel has a density of approximately 7.93 g/cm³, while aluminum has a density of around 2.70 g/cm³. Adjust the general weight formula to incorporate the specific material density for accurate calculations.
Wire mesh may be coated with materials such as zinc (galvanized), PVC, or other protective coatings to enhance durability and corrosion resistance. These coatings add to the overall weight of the wire mesh. For example, galvanized wire mesh will weigh more than uncoated wire mesh due to the additional zinc layer. Consider the weight of coatings when performing calculations.
Heat treatments like annealing or hardening can alter the physical properties of the wire mesh, potentially affecting its weight. While the impact on weight may be minimal, it is still important to account for any changes in material properties resulting from heat treatments.
Temperature variations can cause thermal expansion or contraction of the wire mesh, affecting its dimensions and weight. For example, high temperatures may cause the wire mesh to expand, leading to a slight increase in weight per unit area. Consider the operating temperature conditions when calculating the weight for specific applications.
Humidity can affect the weight of certain wire mesh materials, particularly those prone to corrosion or oxidation. For instance, uncoated mild steel wire mesh may absorb moisture from the environment, increasing its weight over time. Considering environmental humidity is crucial for applications where the wire mesh is exposed to varying moisture levels.
Understanding and accounting for these factors ensures accurate wire mesh weight calculations, aiding in precise planning, cost estimation, and efficient project execution.
Below are answers to some frequently asked questions:
To calculate the weight of stainless steel wire mesh, you need to consider the wire diameter, the mesh number (number of meshes per inch), and the dimensions of the mesh panel. Here are the steps and formulas for different types of mesh:
For square hole stainless steel welded wire mesh, the formula is:
Alternatively, you can use:
For example, if you have a stainless steel wire mesh with a wire diameter of 0.12 mm, a mesh number of 80 per inch, and dimensions of 1 meter by 30 meters:
For rectangle hole stainless steel welded wire mesh, the formula is:
A general formula applicable to any shape is:
For instance, for a galvanized welded wire mesh with a wire diameter of 0.9 mm, a mesh size of 1/2 inch x 1/2 inch, and dimensions of 3 feet by 100 feet:
Key points to remember:
By using these formulas and ensuring all measurements are in the correct units, you can accurately calculate the weight of stainless steel wire mesh for your specific requirements.
The accuracy of wire mesh weight calculations is influenced by several key factors. Firstly, the wire diameter is crucial, as any inaccuracies in measuring it can significantly impact the overall weight. Accurate measurement using tools like a caliper or micrometer is essential. Secondly, the mesh count, which denotes the number of holes per inch, and the aperture size, or the gap between the wires, are critical parameters. These factors determine the density and open area of the mesh, thereby affecting its weight. Precise measurements of these parameters are necessary for accurate calculations.
Additionally, the length and width of the mesh must be measured precisely, as they directly impact the weight calculation. The material density also plays a significant role; different materials, such as stainless steel or copper, have different densities that must be factored into the calculation. Using the correct weight calculation formula is vital, with different formulas required for plain/twill weave wire mesh and Dutch weave wire mesh.
Measurement precision across all parameters—wire diameter, mesh count, length, and width—is crucial to avoid errors that could lead to inaccuracies. Lastly, environmental and handling factors, such as deformation or damage due to improper storage or handling, can indirectly affect weight calculations by altering the mesh’s dimensions. By considering these factors and using accurate measurements and appropriate formulas, the weight of wire mesh can be calculated with high precision.
The wire diameter significantly influences the weight of wire mesh through several key factors. Primarily, the weight of wire mesh is directly proportional to the square of the wire diameter. This means that as the wire diameter increases, the weight of the mesh increases exponentially. The relationship can be represented by the formula: Weight = (wire diameter)² x mesh x length x width. This formula highlights that the weight is a function of the wire diameter squared, indicating a substantial increase in weight with even small increases in diameter.
A thicker wire diameter results in a stronger and more durable mesh, but it also reduces the size of the openings between the wires. This increased material volume contributes to a higher overall weight. Accurate measurement of the wire diameter, typically using a micrometer or caliper, is crucial as it directly affects the weight calculation.
The aperture size, which is the distance between two adjacent wires, is determined by subtracting the wire diameter from the pitch (the distance between the centers of two adjacent wires). While the aperture size itself doesn’t calculate the weight, it is influenced by the wire diameter, which in turn affects the weight.
In practical terms, thicker wires require more material, leading to an increase in the overall weight of the mesh. This is particularly important in applications where weight is a critical factor, such as aerospace or construction industries. Additionally, standard tolerances for wire diameters can cause variations in the final weight of the mesh. For example, specific tolerance ranges for stainless steel wire mesh can affect the final weight.
In conclusion, wire diameter is a crucial parameter that directly impacts the weight of wire mesh. As the wire diameter increases, the weight of the mesh also increases due to the greater volume of material used, enhancing the strength and durability of the mesh.
Yes, you can calculate the weight of wire mesh for different materials using a general formula, but you need to make material-specific adjustments to ensure accuracy. The general formula for calculating the weight of wire mesh typically involves parameters such as wire diameter, mesh number (number of meshes per inch), width, and length of the mesh.
The basic formula is:
This formula is generally applicable for materials like stainless steel, iron, and steel. However, for other metals like aluminum, brass, copper, mild steel, nickel, and phosphor bronze, you need to adjust the calculated weight by multiplying it with specific factors for each material. For instance, aluminum’s weight is adjusted by multiplying with 0.364, and brass by 1.094.
Additionally, the type of mesh can affect the calculation. For square hole mesh, the calculation is straightforward using the formula above. For rectangle hole mesh, you need to consider both the warp and weft mesh numbers and wire diameters.
To illustrate, if you calculate the weight for stainless steel mesh as 17.28 kg, for aluminum, it would be:
17.28 kg x 0.364=6.29 kg
In summary, while the core formula for calculating the weight of wire mesh is similar across different materials, you must consider specific material densities and necessary adjustment factors. Additionally, the type of mesh (square or rectangle holes) can influence the calculation. Therefore, material-specific adjustments and mesh type considerations are essential for accurate weight calculations.
The influence of the material of a wire mesh on its weight primarily manifests in the density of different materials. The materials of wire ropes and wire meshes can be divided into steel wire, nickel-chromium steel, alloy steel, stainless steel, etc. These materials have different densities, thereby affecting their weight.
For instance, a wire mesh made of steel wire, exhibiting excellent strength and durability, is suitable for withstanding considerable tension and pressure, widely applied in the construction industry.
Additionally, the materials of protective meshes usually include steel wire, aluminum alloy, stainless steel, etc. The difference in density of these materials would also result in different weights. Thus, it can be concluded that the impact of the material of a wire mesh on its weight is primarily due to the density differences of various materials.
The selection of the appropriate calculation method depends on the type of wire mesh, such as galvanized wire mesh, stainless steel wire mesh, etc. We can summarize the following points:
For different types of wire meshes, their weight calculation formulas may vary. This indicates that the specific properties of different material wire meshes need to be considered in calculations.
The calculation of wire mesh pieces can be done by software automatically calculating the length according to the material, then multiplying by the width specified in the project. This method is applicable to various material wire meshes, including but not limited to galvanized wire mesh and stainless steel wire mesh.
In terms of construction welding, the calculation method for wire mesh piece specifications reflects in the production of multiple models, sizes, and style types. This means that when selecting the calculation method, the specific specifications and application requirements of the wire mesh need to be considered.
Choosing the appropriate calculation method first requires understanding the type and characteristics of the wire mesh. For galvanized wire mesh and stainless steel wire mesh, etc., the method of software automatically calculating the length and multiplying by the width can be used for calculation. This ensures the accuracy and applicability of the calculation results.
In real-world applications, choosing the most suitable method for calculating the weight of wire mesh requires first considering the specific type of mesh and its use. We can see that different types of mesh have different calculation formulas. For example, the weight calculation formulas for copper mesh and stainless steel mesh are as follows:
Weight calculation formula for copper mesh: Wire diameter × Wire diameter × Mesh count × Length × Width ÷ 2 × 1.07 = kg.
Weight calculation formula for stainless steel mesh: Wire diameter × Wire diameter × Mesh count × Length × Width ÷ 2 × 1.07 = kg.
This shows that the calculation methods for copper mesh and stainless steel mesh are similar, with the main difference being the density difference (1.07) caused by different materials.
For steel aluminum plate mesh, its weight calculation formula is:
Mesh weight (kg): Mesh length ÷ 1/2 short section rectangle × Stem thickness × Stem width × Mesh width × 7.85.
This formula involves multiple parameters such as mesh length, short section rectangle (hole width), stem thickness, stem width, and mesh width, and is suitable for accurately calculating larger areas or complex structures of wire mesh.
Therefore, when choosing the most suitable weight calculation method, it should be decided according to the specific type of wire mesh and its use. If it is copper mesh or stainless steel mesh, the general calculation formula mentioned above can be used. For special types of mesh such as steel aluminum plate mesh, a calculation formula specifically designed for that type of mesh should be used. In addition, cost calculation considerations, such as cost:= mesh weight × plate price + labor cost + circulation cost, are also one of the factors to consider when choosing a calculation method.